THE INFLUENCE OF DENSITY DRIVEN MIXING MECHANISMS ON UREOLYSIS INDUCED CARBONATE PRECIPITATION

Philip J. Salter¹ , James M. Minto¹ , Jay Warnett^2,3 , Katherine J. Dobson¹

¹Department of Civil & Environmental Engineering, University of Strathclyde, James Weir Building, Glasgow, UK; ²International Manufacturing Centre, WMG, University of Warwick, Coventry, UK; ³NXCT - National Facility for X-ray Computed Tomography, The University of Manchester, Manchester, UK

Introduction

Enzyme induced carbonate precipitation (EICP) is a bio-cementation technique that can be used to seal microfractures and pore throats that are inaccessible to cement and chemical based grouts (27), with many similarities to the better-studied microbially induced carbonate precipitation (MICP). Although EICP has been explored in 2D microfluidic flow cells (10, 28) and various engineering applications—such as soil stabilization and strengthening (3, 21, 22), permeability reduction (31), and hydrocarbon-contaminated sand treatment (25)—it is not yet routinely deployed. This is partly due to a lack of necessary understanding of 3D pore-scale precipitation. We therefore cannot predict, control or exploit the distribution of CaCO₃ through time and space using different injection strategies.

Large scale geological sequestration of carbon dioxide (CO₂) is an essential component in tackling climate change (12) and we need at least another 10,000 CO₂ injection wells globally by 2050 (23). At present there are only 26 projects worldwide, most of which only have CO₂ injection/storage to enhance oil recovery. Key challenges preventing more widespread development include the need to prevent CO₂ leakage into the atmosphere or groundwater (4), managing injection into heterogeneous natural rocks, and converting existing hydrocarbon extraction systems for CO₂ injection and storage. Enzyme induced carbonate precipitation (EICP) is a technique that could be used to create spatially targeted impermeable barriers in the subsurface and seal leakage pathways around wellbores (17), and is therefore a key tool in controlling the injection of and preventing the leakage of geo-sequestered CO₂ (and H₂).

Enzyme induced carbonate precipitation involves injection of two reagents – a solution of ureolytic enzyme (usually called the enzyme solution; ES) and a solution of urea and calcium (usually called the cementing solution; CS), both of which have low viscosity. On mixing, calcium carbonate precipitates following Equations 1 to 4.

	(1)
	(2)
	(3)
	(4)

For optimal permeability reduction, an ideal EICP treatment would achieve well mixed fluids and homogenous precipitation of large volumes of CaCO₃. By controlling the injection points and the spatial and temporal evolution of the mixing profile in the sample, it should be possible to control where in the sample precipitation occurs, and therefore how the permeability of the sample changes.

To develop effective and deployable EICP strategies, we need experimental data on how mixing occurs within the pore structure, how this mixing influences the timing and location of CaCO₃ precipitation, and a numerical model capable of predicting this behavior in subsurface systems. Previous studies have observed bulk permeability reductions in soil (18) and fractured rocks (20) but have not quantified the spatial and temporal evolution of the precipitation, or the pore-scale distribution of CaCO₃, therefore numerical modelling of this system remains challenging and largely unvalidated.

Here we exploit high speed laboratory X-ray computed tomography (XCT) to visualize and quantify the spatial and temporal distribution of CaCO₃, capturing precipitation dynamics, flow path migration and the evolving porosity (8, 9, 15). We measure crystal volume and position relative to pore throats and grain contacts, and validate numerical models for permeability, flow velocity and fluid mixing behavior in the pore structure of the experiments. This is carried out with the aim of gaining a fundamental understanding of the EICP process sufficient to design up-scaled injection strategies.

Materials and Methods

In situ observation of enzyme induced carbonate precipitation

The enzyme solution (ES) was prepared from 12 g/L urease active jack bean meal¹, and syringe filtered (<0.45µm) after 30 mins homogenization. Jack bean meal was used as it is 70-90% less expensive and has lower urease activity (1500 U/g) than purified urease sources, allowing a slower reaction rate that has been shown to lead to more compact and harder CaCO₃ (6). The cementing solution (CS) was made by dissolving 4M urea and 2.67M calcium chloride in deionized water. The CS pH was adjusted to 6.89 using 4M HCl prior to injection to delay the immediate onset of precipitation (after 5, 16).

Custom made 3D-printed (5 mm diameter, 0.39 cm³ volume) flow cells (Fig. 1) were filled with quartz sand (Sigma Aldrich, silica content ≤100%, particle size range of 210 - 297 µm), with a porosity of 39%. The columns were saturated with a 3 g/L NaCl solution to simulate a subsurface brine and mounted into a Tescan UniTOM XL lab scanner (University of Warwick, WMG). A total of 1.5mL each of CS and ES were simultaneously injected through the two inlet ports (Fig. 1) at a combined flow rate of 1.0 mL/min, corresponding to approximately 6 pore volumes/min. The ES entered the sample at a single central feed point surrounded by the 4 CS feed points (Fig. 1b). After 3 minutes of injection (equivalent to 18 pore volumes), the flow was stopped, and XCT data were collected.

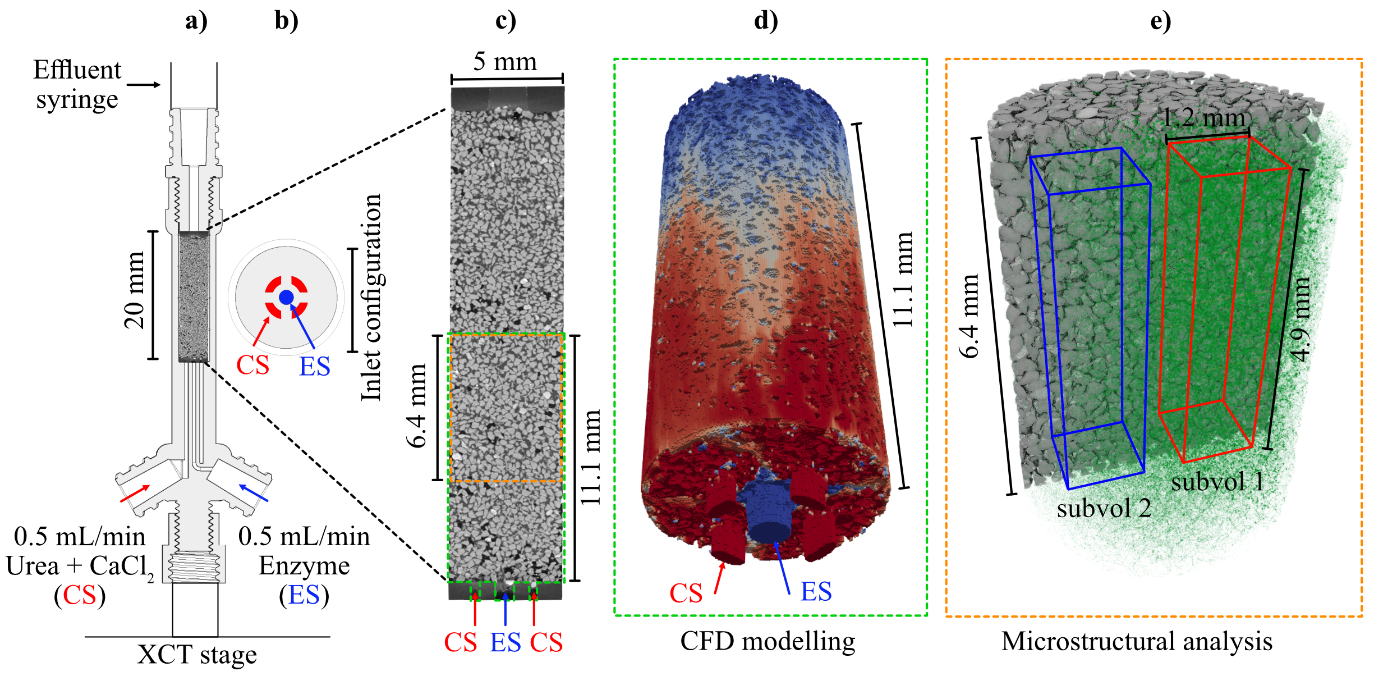
Figure 1: Experimental setup, analysis and modelling: a) 3D printed flow cell, b) inlet configuration showing urea/calcium chloride (red) and enzyme (blue) entry points, c) vertical slice through entire sand pack volume, d) 3D rendering of CFD modelling volume, and e) imaging window captured during sequential scans showing sub-volume 1 (red), sub-volume 2 (blue)

All XCT data were collected at 40kV and 15W/375 µA, with 1440 projections/scan (205 ms exposure time). Twelve scans were acquired over a 1-hour period with each scan lasting 5 minutes. Each scan began immediately after the previous one was completed. Crystal growth was continuous over the scanning period so there will be a difference in the sample structure at projection 1 and at projection 1440. This difference will mean some blurring of the data. A time period of 5 minutes per scan ensured this difference was minimized and that scans could be reconstructed with minimal blurring artefacts, while still seeing CaCO₃ growth that was measurable. The proprietary Tescan reconstruction code generated 3D datasets with 8.156 µm resolution (voxel edge length). Image processing and analysis were completed in Avizo^®2 and the full workflow is shown in Appendix Figure A1 (available online).

Image analysis

The sample remained stationary between scans; however, to ensure precise spatial alignment over time, the data were registered (26) and an edge-preserving denoising anisotropic diffusion filter (2) was applied. A post reconstruction beam-hardening correction was also applied to each dataset. Segmentation was performed using the histogram-based Auto Thresholding module in Avizo (19) to minimize human bias when processing datasets with bulk greyscale values that change over time due to precipitation (App. Fig. A1, available online). The binary map of the pore phase generated through segmentation was inverted to produce a binary map of the solid phases. The similarity of the attenuation (greyscale) prevented the segmentation of the CaCO₃ from the quartz. The quartz does not change through time and there is no CaCO₃ at t=0. The CaCO₃ volume was calculated by subtracting the t=0 scan (quartz only) from the segmented quartz + CaCO₃ in later scans (Fig. 2). The porosity was determined by calculating the volume fraction of the non-solid phase relative to the entire cylinder volume.

Figure 2: Segmentation of solid phases and calculation of CaCO₃ by subtraction of t=0 (quartz only) from t=n (quartz + CaCO₃).

The volumes and positions of the crystals were measured from the binary maps of CaCO₃. We use the term “crystal” to refer to each individual object in the binary map, though some may actually be crystal clusters that would only be distinguishable at higher resolution.

The pore network morphology was determined at t=0 using a separation based on a Random Walk Distance Map (1). Pore volume, geometry and coordination numbers were measured for each pore, and pore throat locations were identified. While the sand grains remain stationary, precipitation alters the volume and geometry of the pores, which could potentially change the number and location of pore throats. We therefore use the pore throats defined at t=0 for all t≠0 datasets, applying the segmented t≠0 pore network as a mask to the t=0 separated 3D pore map (see Figure A1, available online). Mapping these properties over time onto a consistent geometry enables the quantification of volume and geometry changes at the pore scale. The location, area, and geometry of the pore throats at t=0 were extracted from the Local H-Maxima output (see Fig. A1 in the Supplementary Material, available online). The distance from every point within the pore network to the nearest throat was then calculated using a Distance Map. The distance of each CaCO₃ crystal to the nearest pore throat was then extracted through Label Analysis applied to the distance map output, masked by the 3D CaCO₃ location map (See Fig. A1 in the Supplementary Materials for details, available online). At each time point, the permeability of the pore network was calculated using the Absolute Permeability Simulation available within the XLab Simulation package of Avizo.

A second Random Walk Distance Map was applied to the inverted pore network at t=0, and the volume, surface area, sphericity, and coordination number (i.e. number of solid-solid contact points) of the quartz grains were measured using a Label Analysis.

By integrating the pore geometry and CaCO₃ 3D location maps with the permeability simulation outputs, we can determine the mean velocity of flow in each pore, through each pore throat, and at each crystal location during the initial injection phase (Fig. 3). Pore and CaCO₃ analysis and Absolute Permeability Simulations were also performed on two smaller sub-volumes selected from different regions of the sample (Fig. 1).

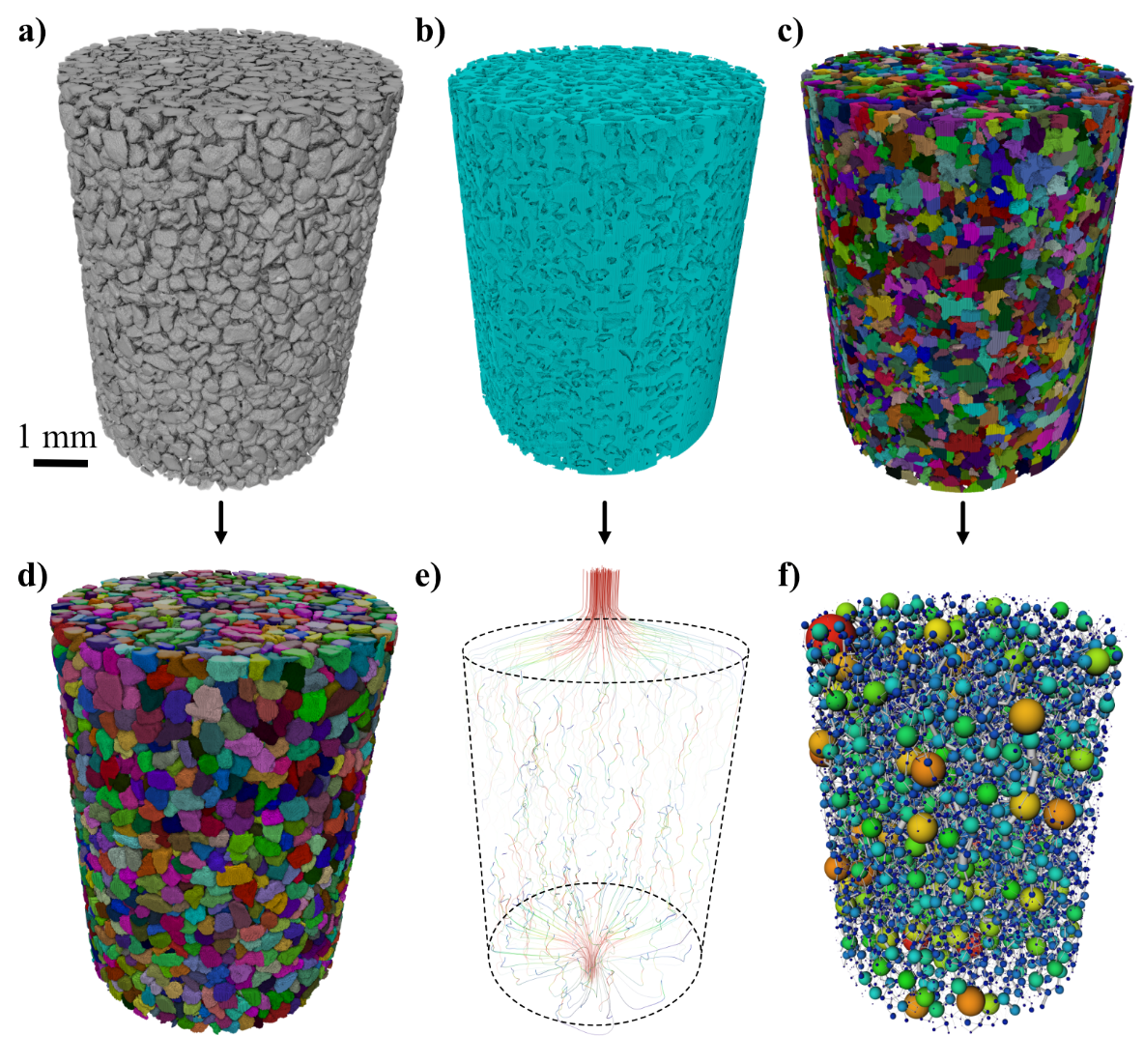
Figure 3: 4D Image processing workflow: a) binarized solid regions, b) connected pore space,
c) separated pores by random walk distance map, d) separated grains, e) output streamlines from absolute permeability simulation, and f) pore network model.

Uncertainty in the image analysis

The small volume of the CaCO₃ crystals, ranging from 542 µm³ (a single voxel) to 4.5x10⁸ µm³ (mean = 6766 µm³), along with the common formation of crystal clusters, is the primary source of uncertainty in the quantitative data. The partial volume effect comes from defining any irregular particle as a group of voxels. The greyscale values of voxels that intersect the surface of the particle will be proportional to the relative volume of the particle and the surrounding media within the voxel. As the segmentation process will include or exclude a voxel based on that greyscale value, the binarized (segmented) data will locally (at the voxel scale) over or underestimate the location of the particle surface. For CaCO₃ crystal clusters, this may be further complicated as the internal voxels can have both particle and pore fluid within them. The value of the uncertainty on any individual particle and any particle population can be calculated (14). The pores and sand grains are all large relative to the voxel size (mean volume of 4180 and 18200 voxels respectively), thus the uncertainty cannot be seen when plotted on the size distributions.

Another potential source of uncertainty is the combination of spatial and temporal resolution. While we observed no evidence of crystal motion during the experiment, nor of nucleation and growth away from the sand grain surfaces, the resolution of the images may prevent the capture of very small crystals. However, crystals are observed to form on all sides of sand grains with no clear preference for the upper surface, suggesting that nucleation primarily occurs directly on the grain surfaces rather than in the solution, followed by settling on the tops of grains. Each 3D acquisition takes 4 minutes and 55 seconds, with a new scan started every 5 minutes. As a result, data reconstruction could be affected by changes in CaCO₃ volume during a scan. However, we can see measurable differences in crystal volume between time points and find minimal blurring artefacts in the data, suggesting that individual datasets are significantly impacted by crystal growth. We therefore assume that any effect is captured in the partial volume effect in the reconstructed data.

Modelling of fluid mixing

Fluid mixing was simulated using the computational fluid dynamics software OpenFOAM, with a domain extending from the inlet to the top of the dynamic imaging window (Fig. 1). The injection parameters were designed to replicate experimental conditions, where the four outer inlets injected CS (density = 1234 kg/m³, viscosity = 2.1157×10^-6 Pa∙s), while one central inlet injected ES (density = 998 kg/m³, viscosity = 1×10^-6 Pa∙s). The mesh was generated from a full sample scan with a voxel edge length of 13.768 µm; however, this resolution was computationally prohibitive for dynamic flow simulations. Down-sampling by a factor of 2 resulted in a voxel edge length of 27.536 µm, which balanced computational efficiency with sufficient resolution to capture flow behavior while enabling feasible simulation times. A mesh independence verification was conducted by comparing Absolute Permeability Simulations for the original (13.768 µm) and down-sampled (27.536 µm) meshes. The sensitivity analysis on permeability showed that while down-sampling altered the simulated permeability value by 18%, it did not significantly affect flow path dynamics (Appendix Fig. A2, available online). The code used to convert voxel data into a mesh readable by OpenFOAM, with appropriate boundary patches, was written as an ImageJ script implemented in Fiji (24), following the methodology outlined in Section 3.5 of Willems et al. (29).

The twoLiquidMixingFoam solver within OpenFOAM was used to model injection and subsequent density-driven flow of the miscible ES and CS. The solver employed second-order spatial discretization schemes for key terms, ensuring accurate representation of flow dynamics. Temporal discretization was handled using the first-order implicit Euler method for stability in transient simulations. A detailed list of parameter settings and schemes is provided in Table A1 (Appendix A, available online).

The focus was placed on adjusting density and viscosity parameters, as these were critical for capturing mixing behavior, while all other parameters were retained from the validated twoLiquidMixingFoam tutorial. The post-injection flow phase was also modelled to account for the density-driven mixing during crystal formation.

RESULTS

Quantification of EICP in 4D

Data were collected across 12 time points during crystallization (no injection). The sensitivity analysis on permeability showed that while down-sampling did alter the simulated permeability value (18%), it did not significantly alter flow path dynamics (Appendix Fig. A2, available online). The injection points are lower than the imaging window (Fig. 1) and it was therefore anticipated, due to the miscibility of the two fluids, that sufficient mixing would have occurred beneath this to promote uniform crystallization across the imaging region. The simulated permeability across the red sub-volume 1, where ~5% CaCO₃ eventually formed, is reduced much more rapidly than the blue sub-volume 2 or the whole domain.

Figure 4 summarizes the simulated permeability and volume fraction of CaCO₃ for the full imaging volume and sub-volumes 1 and 2 at 20, 35, 50 and 65 minutes, highlighting the localized effects of CaCO₃ precipitation on hydraulic properties.

Porosity evolution during EICP

During the first 20 minutes of the reaction, the vertical distribution of CaCO₃ is relatively homogenous. However, as the reaction progresses, the volume fraction of CaCO₃ increases gradually from inlet to outlet (Fig. 5). Once nucleated, the crystals formed in the lower portion of the column (<5 mm) showed minimal volume increase over time, while those formed towards the outlet continue to grow. To quantify porosity evolution along the flow direction, we plotted the 2D percentage of CaCO₃ from the base of the imaging region (near-inlet) to its top (Fig. 5).

a)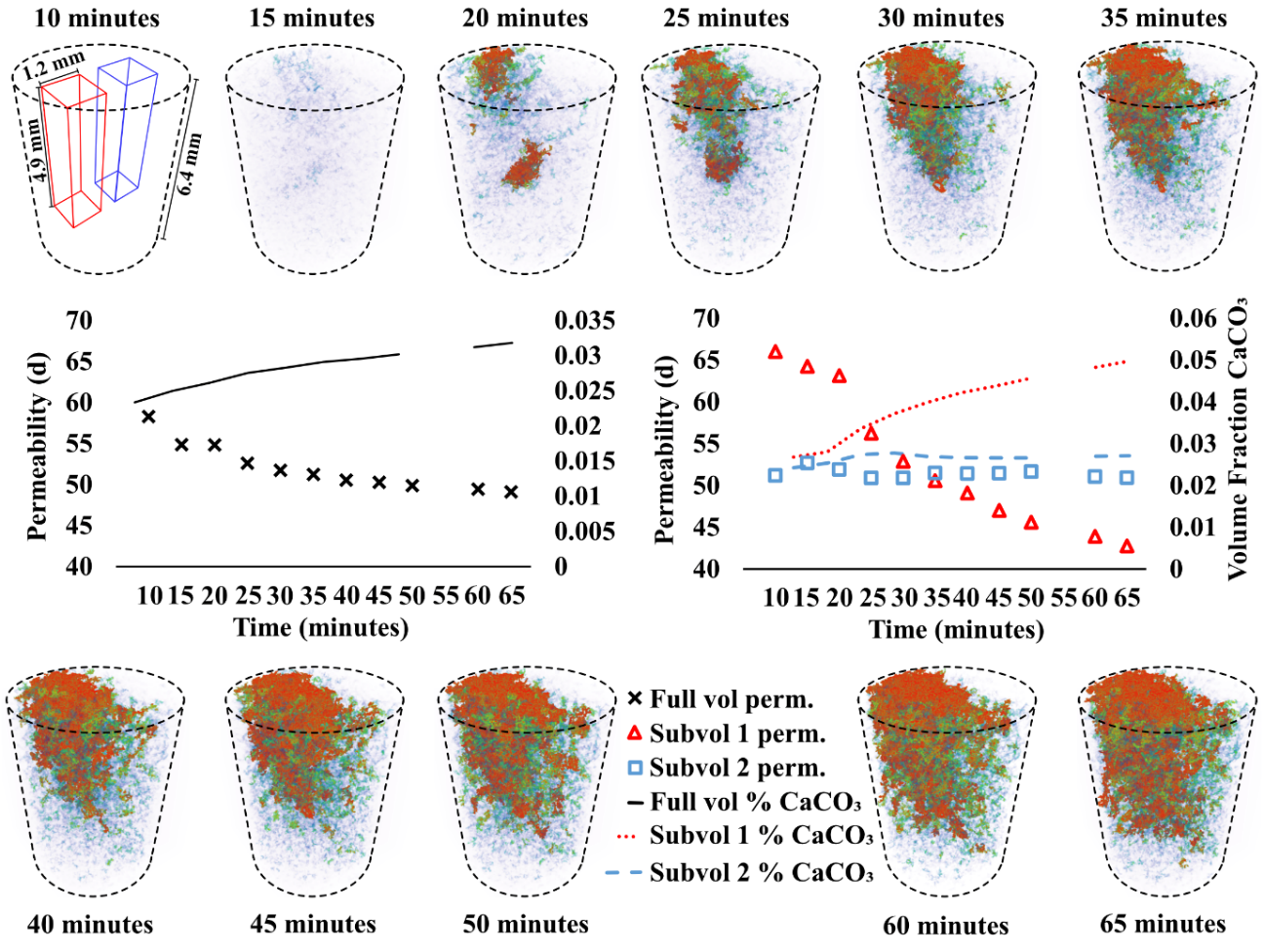
b)
c)
Volume Time (mins) Vol. Fraction CaCO3 Simulated Permeability (Darcy) Full Volume 20 0.0250 54.85 35 0.0283 51.25 50 0.0302 49.86 65 0.0318 49.12 Sub-Volume 1 20 0.0280 63.14 35 0.0400 50.58 50 0.0455 45.61 65 0.0498 42.77 Sub-Volume 2 20 0.0254 51.92 35 0.0269 51.48 50 0.0266 51.66 65 0.0271 50.93
Figure 4: CaCO3 precipitation over time: a) Spatial distribution of CaCO3 over time with crystals colored with red representing the largest and blue the smallest volumes. b) Graph of permeability/time/volumetric % CaCO3 for the full volume (black), highly precipitated sub-volume 1 (red), and low precipitation sub-volume 2 (blue). c) Simulated Permeability and Vol. Fraction CaCO₃ for the Full Volume and Sub-volumes at Selected Time Points During EICP.

While the evolution of CaCO₃ distribution is explored relative to column height in Figure 5a, the 3D distribution of CaCO₃ can be more effectively visualized by plotting the average radial and axial concentration for each individual pixel (Fig. 5b). The main precipitation zone forms a cone-like shape, with the highest concentrations of CaCO₃ occurring centrally and towards the outlet.­ The position of precipitated CaCO₃ relative to quartz grain surfaces, as determined by random walk distance map, is explored in Figure 6.

a)
b)
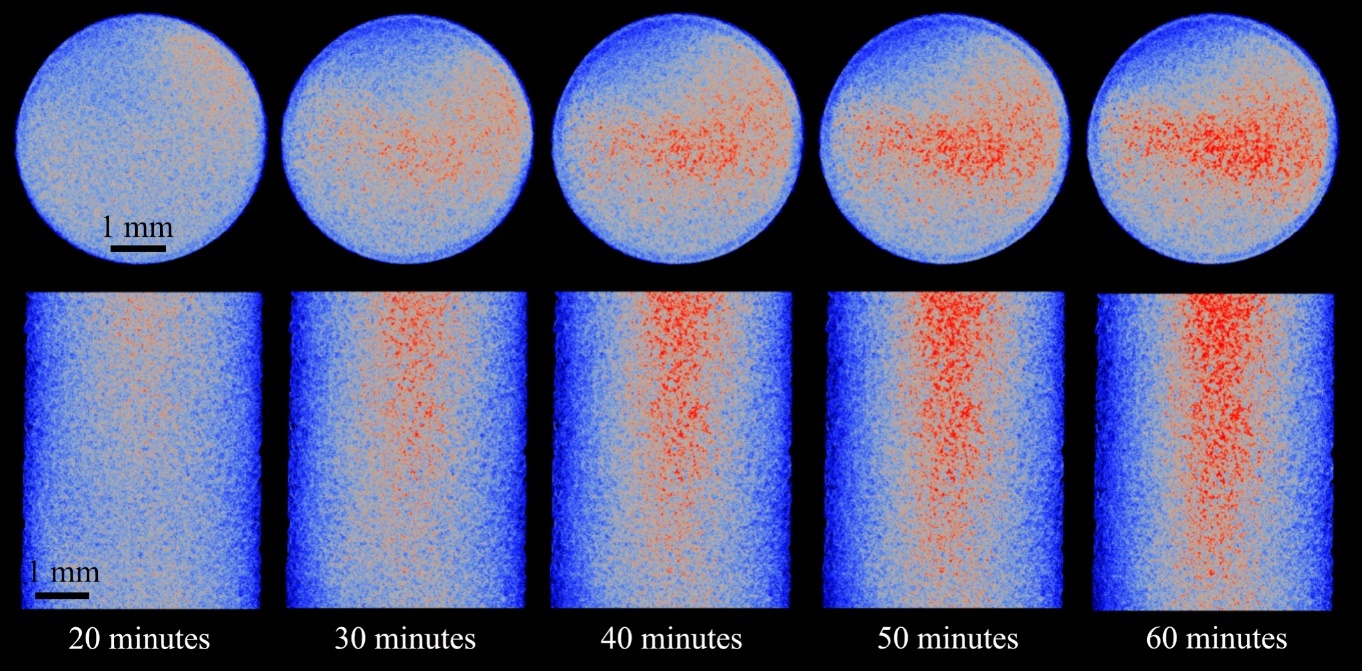Figure 5: Distribution of CaCO3 over time with: a) Column depth - The inset images are at 65 minutes and approximately 0.4mm (left) and 6.1mm (right) from the bottom of the dynamic imaging window with CaCO3 colored red, b) radial and axial CaCO3 distribution (red) over time.

Unlike MICP, where cells tend to attach at grain contact points before acting as nucleation sites for crystal growth (i.e. the solution immediately around them becomes supersaturated with respect CaCO₃) (16), we observe many small crystals nucleating throughout the column, before growing out into open pores on existing CaCO₃ (Fig. 6f). This precipitation mechanism (schematically represented in Fig. 6d) appears to be more dominant than CaCO₃ growth at grain contact points (Fig. 6e). The mean distance map values for CaCO₃ that then forms between scans (Fig. 6b) shows a subtle upward trend in crystals growing towards open pores over time rather than continued grain surface growth. By coloring CaCO₃ crystals by their mean distance map value (Fig. 6f) we see that the crystals that grow towards open pores (i.e. warmer colors) are primarily found within the main precipitation band. The continued growth in this region is therefore on pre-existing CaCO₃.

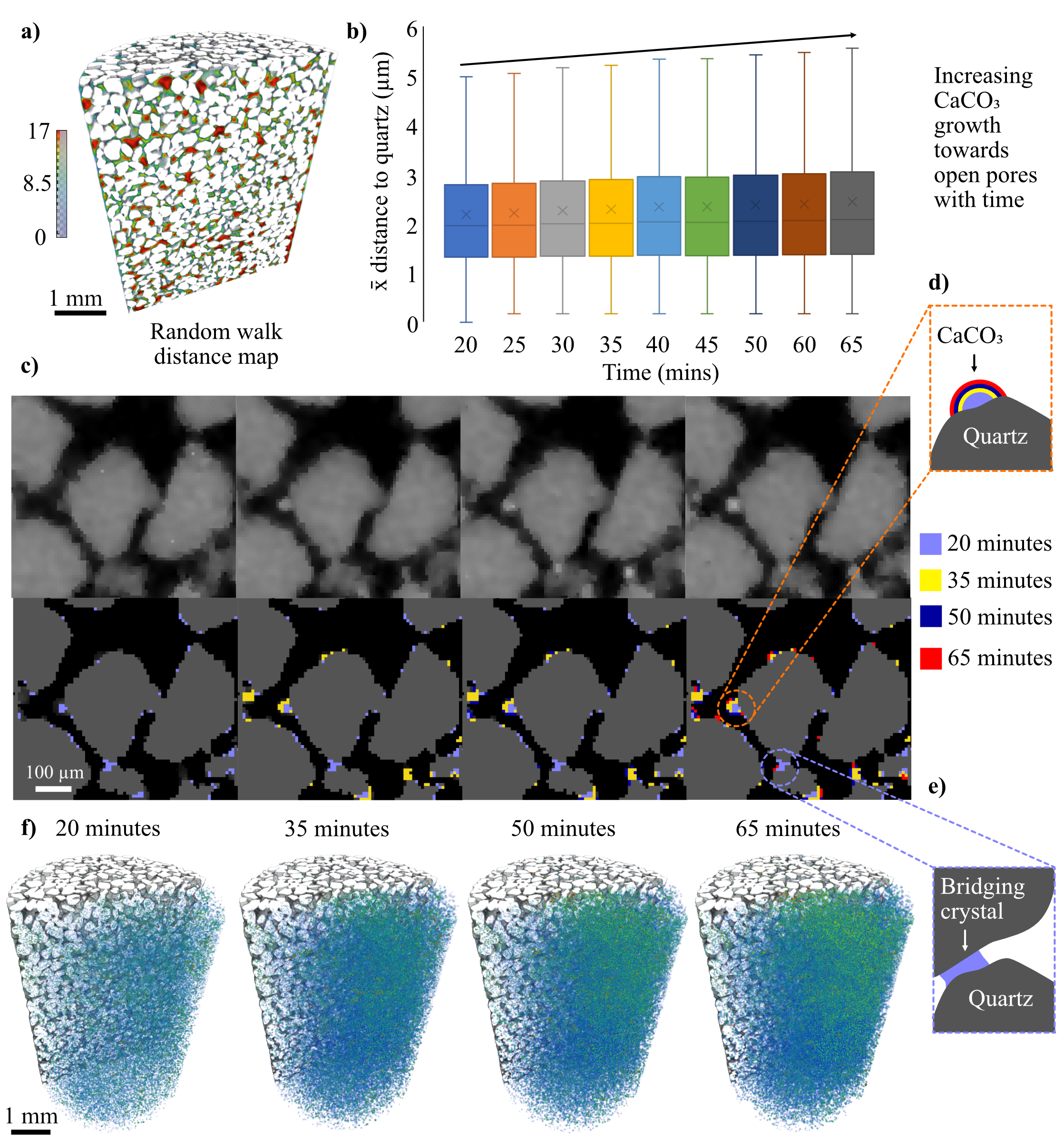Figure 6: Crystal locations relative to quartz grain surfaces as determined by random walk distance map. a) Random walk distance map with near grain surfaces colored blue and open pores (red). B) Box plots of the mean distance of new CaCO3 (grown between scans) to quartz grain surfaces for each time point. c) Zoomed in view of XCT data showing how crystals form over time. Schematic of CaCO3 growth into d) open pores and e) grain contact points. f) Crystals colored by distance map value over time with coloring as per (a).

Absolute permeability evolution and mixing during EICP

Absolute permeability refers to the ability of a porous material to transmit a single-phase fluid and is characterized by a constant coefficient that relates fluid flow and material parameters in Darcy's law (Eq. 5):

	(5)

Where the global flow rate that goes through the porous medium is represented by , which is measured in units of m³/s. The cross-sectional area of the sample through which the fluid flows is represented by and is measured in m². The dynamic viscosity of the fluid flowing through the sample is represented by and is measured in Pa∙s. The pressure difference applied across the sample is represented by and is measured in units of Pa. represents the length of the sample in the direction of flow and is measured in m. Permeability, with units in m², is therefore a function of the pore geometry and connectivity within the sample, and a bulk value of permeability can be obtained for the entire sample by experimentally measuring the pressure drop for a given flow rate, as is typically done for cylindrical cores in a core holder.

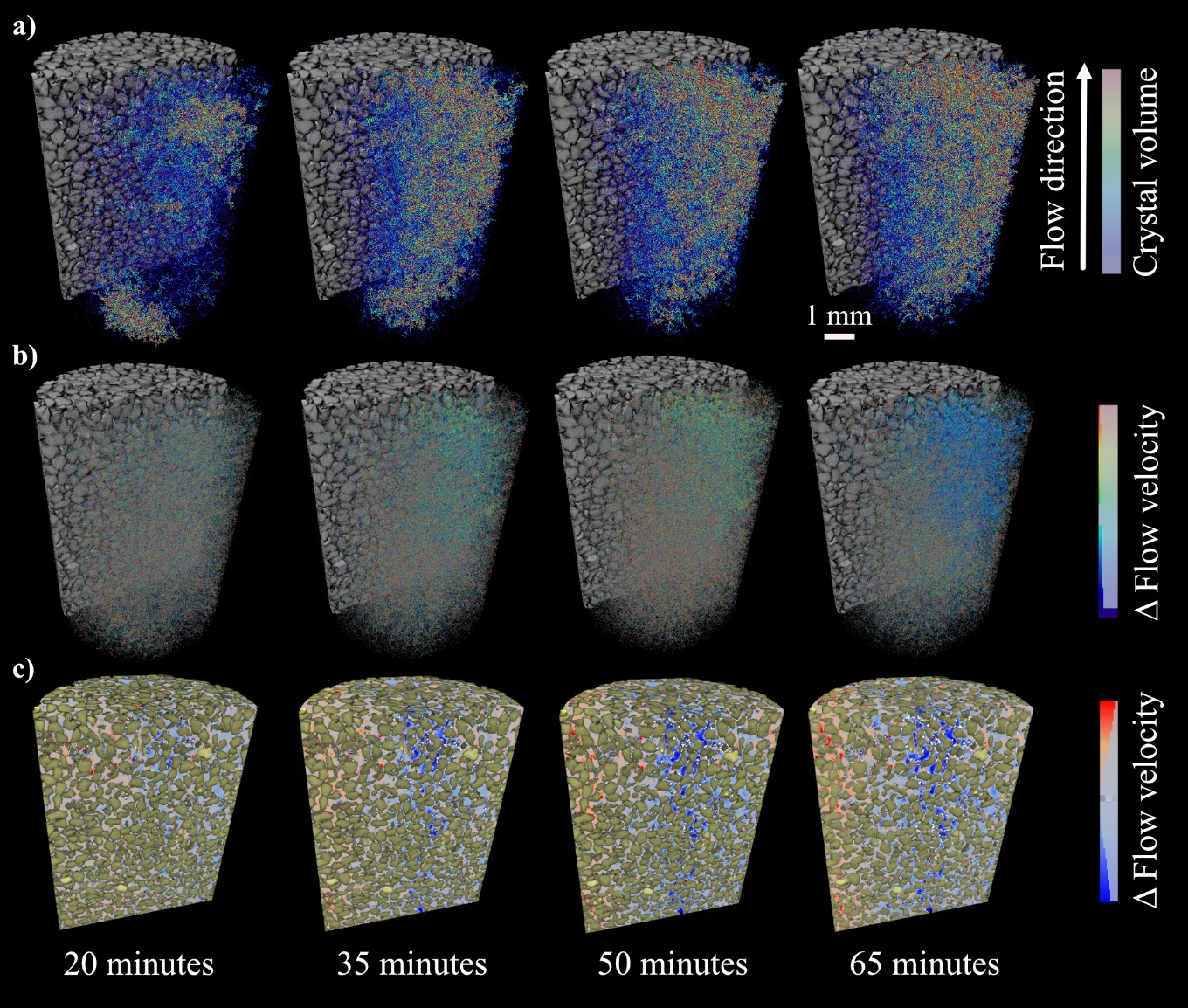
Figure 7: The effect of enzyme induced CaCO₃ on flow: a) crystals are colored by volume, b) their effect on simulated flow velocity relative to t=0 and, c) with crystals colored white, and pore space colored by the flow velocity at t≠0 minus the flow velocity at t=0 from flow simulations.

Permeability can also be estimated numerically based on XCT derived pore geometry and connectivity together with simulated fluid flow and pressure drop across samples of any shape or size without limitations imposed by the core holder design or pressure sensor resolution. In this study, the Avizo XLab Simulation module was used for the determination of the absolute permeability with the added benefits that flow paths are also calculated and, rather than a single bulk measure of permeability, multiple permeabilities can be calculated for different regions of the sample.

In addition to simulation of the initial (pre-EICP) pore geometry, permeabilities were also calculated at different time points during the static EICP reaction period to understand how the precipitating CaCO₃ and evolving pore geometry were shaping the hydraulic properties. The results of permeability/porosity and permeability/time calculations are shown in Figure 4.

By running absolute permeability simulations at each time point, the output velocity field can be used to visualize and quantify the effect that each individual crystal would have on flow at that particular instance in time (Fig. 7).

The location of the extracted sub-volumes is shown in the Figure 1e. While the initial permeability of sub-volume 1 (61.4 Darcy) is higher than that of sub-volume 2 (46.4 Darcy), it experiences a 37.1% reduction in simulated permeability over the course of the experiment. There is a negligible (0.8%) reduction in permeability within the blue sub-volume 2. The full imaging volume experiences an intermediate reduction (11.4%) as a result of both regions. Flow is diverted to the column's peripheries as crystals form in the central region, shown by the red areas of the pore space in Figure 7c at 65 minutes. We hypothesize that ES and CS were mixed sufficiently within sub-volume 1 to induce rapid CaCO₃ precipitation and the altering of flow paths (Fig. 8), but that fluid mixing was limited within sub-volume 2, resulting in less precipitation. This is explored further in Section 3.3.1.

Overall, these observations suggest that the impact of EICP on porosity and permeability in sand is highly dependent on the spatial distribution of CaCO₃. As expected, regions with high crystal growth experience a greater reduction in permeability compared to regions with minimal crystal growth.

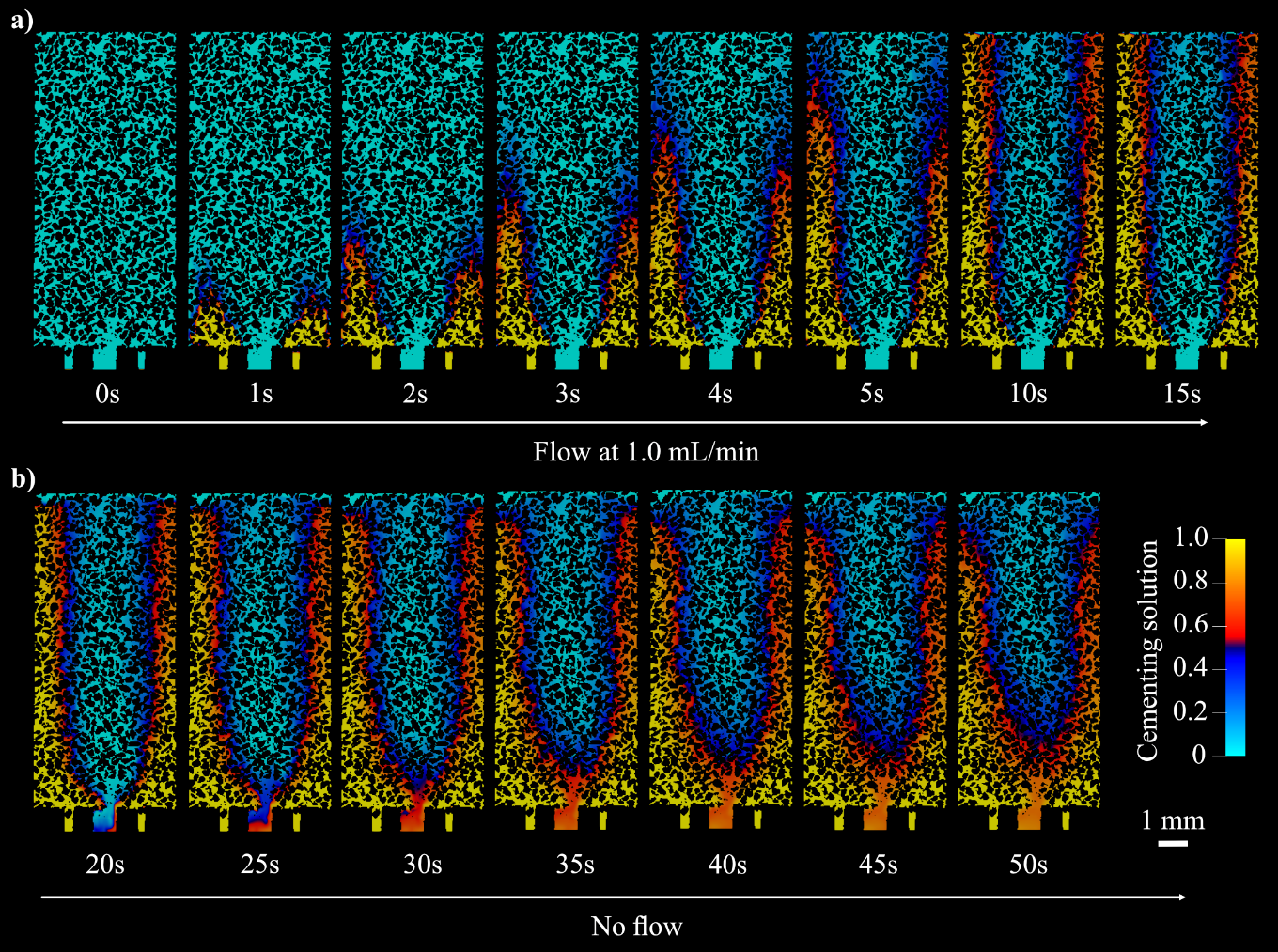
Figure 9: Cross sectional view of enzyme and cementing solution mixing during a) flow of 15s, at which point the injection reaches a steady state, and b) the static period when crystallization occurred.

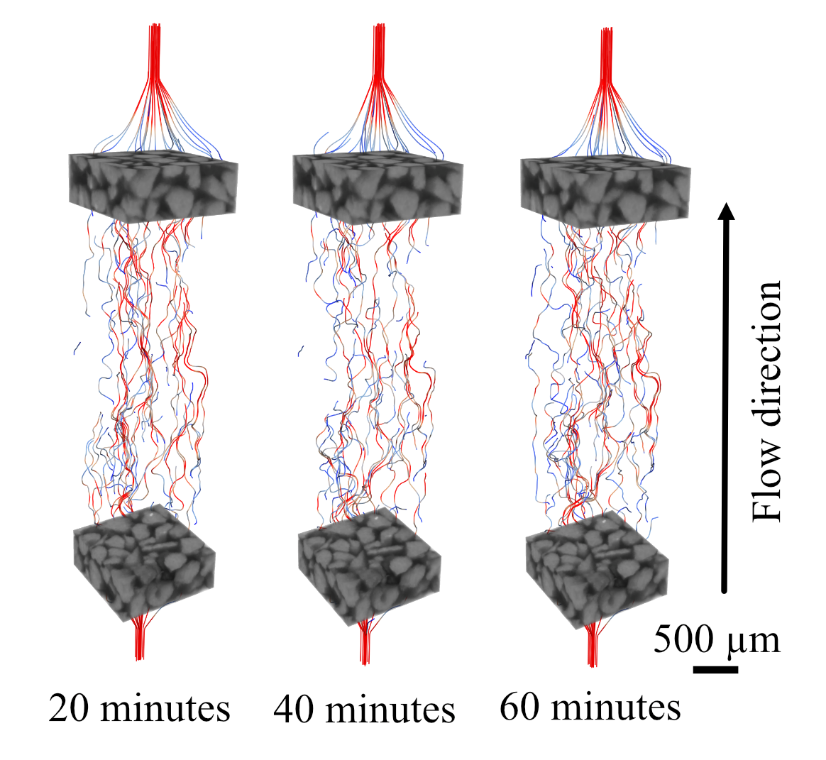
Figure 8: Streamlines of flow paths across high precipitation sub-volume 1 over time.

Simulation of fluid mixing

The distinctive cone-shaped crystal region can be better understood by simulating the mixing of CS and ES within the sample. We also simulate the fluid behavior after flow cessation during imaging. Three mechanisms hinder uniform mixing in the pore space. First, the smaller cross-sectional area of the central inlet (0.486 mm²), used for injecting ES, compared to the four outer inlets (0.760 mm²) used for CS injection, results in a higher flow velocity. This leads to an initial cone-like geometry of the enzyme fluid field (Fig. 9a). Second, the higher kinematic viscosity of CS physically inhibits further mixing. Third, when flow stops, density-driven currents cause CS to settle at the lower part of the sample, reducing the available surface area for diffusion of urea and calcium ions, while improving advective mixing (Fig. 11b). The observed fluid flow behavior is shown in Figure 9. Note that the simulation was carried out in 3D and mesh generated as described in Section 4.2.

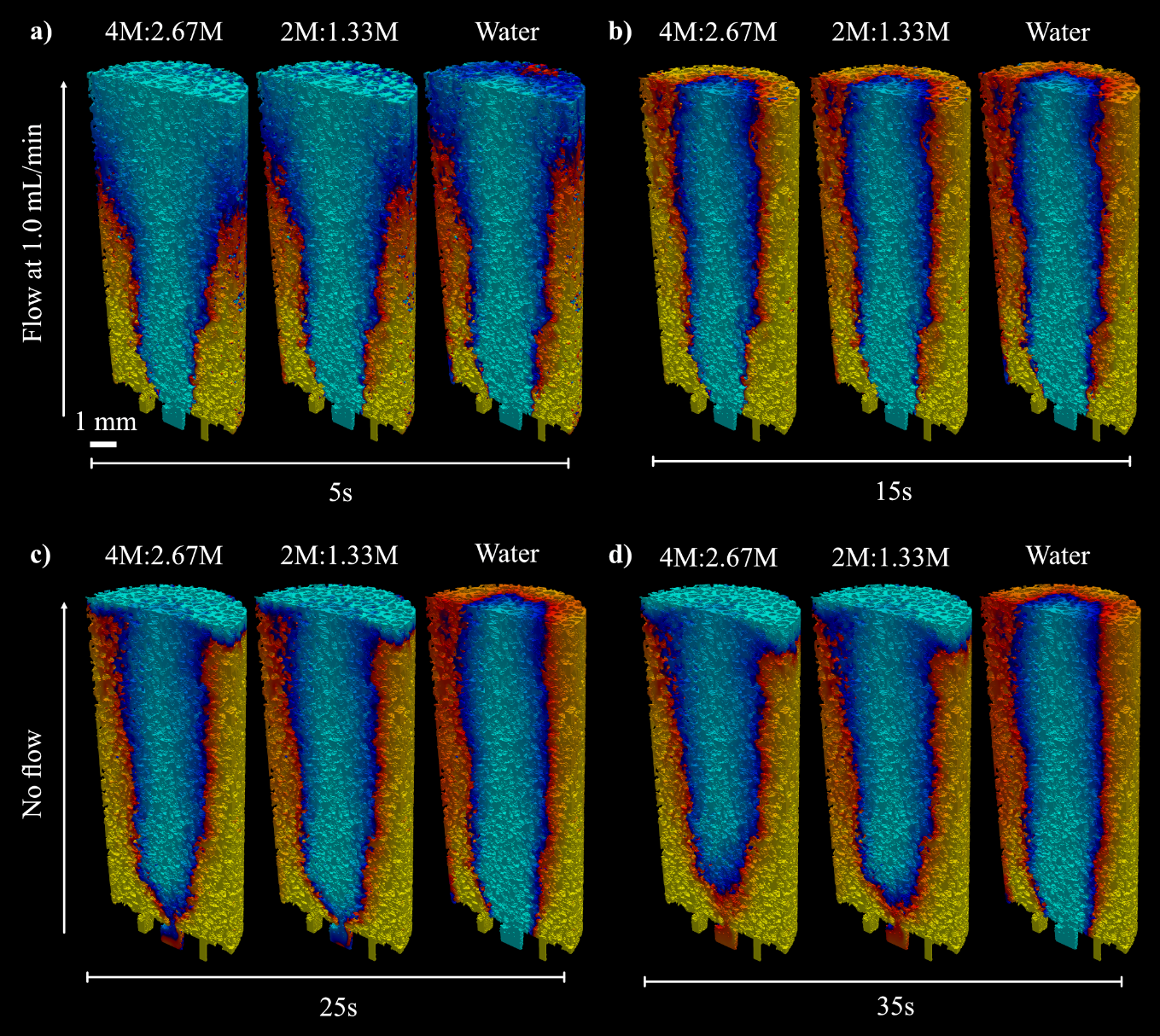
Figure 10: Mixing of fluids under different urea:CaCl₂ cementing solution concentrations. a) 5s of flow, b) 15s of flow, c) 10s after flow cessation, d) 20s after flow cessation.

The simulations were repeated to assess if a lower concentration of cementing solution would improve fluid mixing due to a reduced difference in density and viscosity between CS and ES. This entailed adjusting the fluid properties (kinematic viscosity and density) of the CS in the model to correspond with those of a) a 2M urea, 1.33M CaCl₂ solution, and b) water. The outcomes of these simulations are shown alongside the initial simulation of the experimental setup in Figure 10.

In the early stages of flow (5s) the breakthrough of CS to the top (outlet) boundary is earlier for water than the more concentrated CS. The injection flow rate is the same in all examples therefore as CS concentration increases, the proportion of the porosity occupied by the CS also does. This is due to the gravitational effect of the denser solution “pooling” towards the inlet boundary during flow and potentially viscous displacement. After 15s, the flow is turned off to simulate the no flow period in which crystals formed. From this point, we observe density driven flow forcing CS downwards into an inverse cone shape. The resultant enzyme field (light blue) closely resembles the geometry of the observed crystallization (Figs. 4-7).

To better quantify these different flow mechanisms, we monitored the standard deviation and mean of the CS field over time to track the evolution of mixing (Fig. 11).

The standard deviation (std_dev) is a measure of the spread from the average CS value. A lower std_dev represents more elements closer to the mean value, and therefore better mixing. The slight drop in std_dev once CS reaches the outlet boundary (3-5s), is due to CS branching radially inwards towards the center of the cylinder (Fig. 10a-b), which encourages better mixing. After this point (~7.5s), the std_dev and mean values stabilize under all CS conditions. When flow is turned off at 15s there is a relatively larger drop in std_dev for run-1 and run-2 than run-3, suggesting that density driven flow is promoting mixing, particularly towards the bottom of the flow cell (Fig. 10d). The inset boxes (Fig. 11b) show that the difference in std_dev between the 4M:2.67M and water cases reduces from 0.0128 at 15s to 0.0091 at 40s.

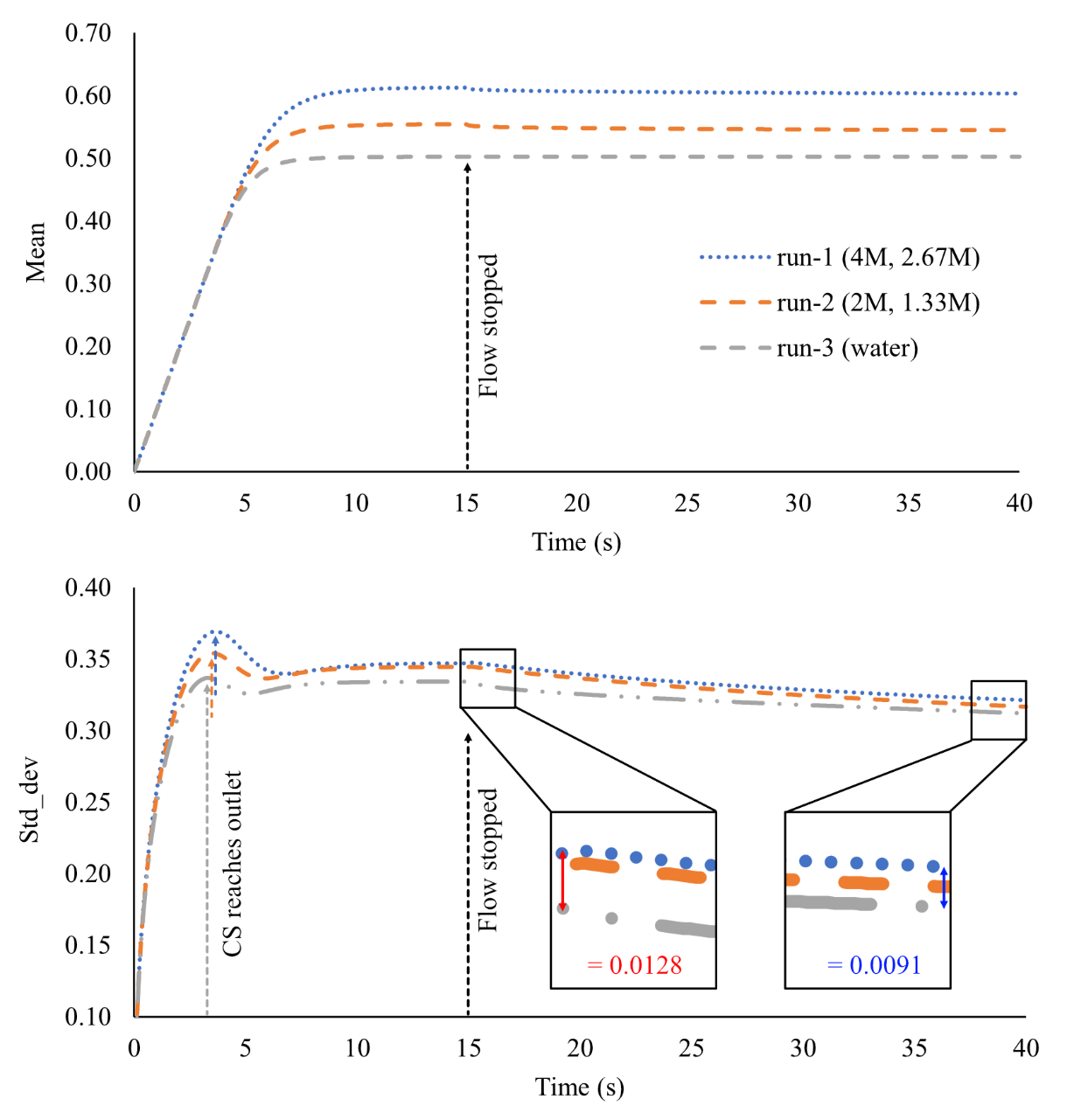
Figure 11: Mixing of fluids under different cementing solution concentrations. Top: Mean CS over time, Bottom: standard deviation over time.

In summary, reducing CS concentration is unlikely to change the observed crystallization geometry (Fig. 10d, 4M:2.67M to 2M:1.33M), but is more likely to reduce the volume of precipitated material through lack of available CO₃^2- and/or Ca²⁺ ions.

DISCUSSION

Comparison with previous permeability measurements and simulation

Our finding that crystal growth primarily extends out into open pores rather than concentrating at grain contact points suggests that a larger volume of CaCO₃ is required with this EICP injection strategy to achieve a similar reduction in permeability as MICP in a similar porous media and at the same CaCO₃ vol% (11). However, permeability reduction following MICP is often due to biomass formation, which is not a permanent plugging agent (18). Further, the urease enzyme is more likely to penetrate smaller pore throats due to its nanoscale proportions (~9 nm) and is therefore more suited for applications in microfractures, and where a greater treatment extent is required, for instance sealing leakage pathways around a CO₂ storage injection well.

We have demonstrated that CaCO₃ precipitated after a single EICP cycle is sufficient to divert flow during subsequent cycles, thereby shifting precipitation to less well-treated regions. Consequently, we anticipate that precipitation will become more homogeneously distributed in porous media over repeated cycles.

Implications for future treatment strategies

Through targeted mixing across a salt gradient (e.g. by perforating injection casing at different depths and injecting CS through the upper perforation and ES through the lower one), we may be able to create subsurface barriers to flow using the described methods. Mixing solutions directly within the rock rather than in the wellbore, surface, or injection tubing reduces the risk of wellbore scaling and encourages improved penetration of injection solutions into the rock formation. Several single-phase injection strategies that allow mixing of CS and enzyme/bacteria prior to injection have also been explored (5, 7, 30). However, these approaches may face challenges, such as wellbore scaling, unless water is injected between treatment cycles to mitigate this issue. Our findings indicate that density currents, which form once flow is turned off, significantly influence mixing behavior and consequently the location of precipitated CaCO₃. While the small simulation volume used in this study is largely affected by the boundary walls of the flow cell, our results align with previous studies on MICP in shallow submerged conditions (13), confirming that density-driven flow controls the location of CaCO₃ precipitation. In a future paper, we will investigate larger-scale mixing behavior of the proposed EICP treatment strategy for near-wellbore environments using numerical modelling. We will also compare this with single-phase injection methods to assess their potential for achieving more homogeneous and widespread precipitation. Additionally, future work will consider the impact of varying subsurface conditions such as heterogeneity in permeability, temperature gradients, and varying salinity levels, all of which could further influence the effectiveness of these treatment strategies.

CONCLUSIONS

The study investigated the kinetics of enzyme induced CaCO₃ formation. High speed XCT imaging allowed quantification of the distribution of CaCO₃ precipitates along the diameter and height of the column over time. Computational fluid dynamic modelling from the XCT data enabled qualitative and quantitative analysis of fluid mixing and density driven flow at experimental and theoretical urea/CaCl₂ concentrations. The main conclusions of the study are:

1. Porosity Evolution: More precipitation occurs downstream from the injection point, with limited precipitation in the inlet region due to poor mixing. Precipitates form mainly within the enzyme fluid field rather than in the cementing solution field, showing no obvious relationship with grain contact points. After initial nucleation (within 20 minutes), crystals preferentially grow on existing CaCO₃.

2. Permeability Evolution: Flow simulations indicate that overall permeability reduction is low (-11%) within the full volume. However, in more highly precipitated regions, a 37% reduction is possible within 65 minutes following a single injection cycle. A mostly linear reduction in permeability is observed, closely following the increase in CaCO₃ precipitate volume percentage.

3. Fluid mixing: CFD modelling indicates that the observed crystallization geometry is influenced by density-driven flow once injection ceases. Lower concentrations of urea/CaCl₂ are unlikely to alter this observed geometry but may reduce the volume of precipitated material, thereby affecting permeability reduction.

4. Multiple treatments: While only a single EICP treatment cycle was injected here, the spatial evolution in permeability during that cycle suggests that flow during subsequent cycles would take a different route through the porous media. This could act to localize CaCO₃ precipitation in different regions during each cycle with the result that treatment becomes more uniform over time.

In addition to this density driven mixing mechanism, other factors, such as permeability heterogeneity and environmental conditions, are likely to influence treatment effectiveness. These were not explored. Nonetheless, this work highlights the potential of combining high-speed XCT imaging with CFD modelling to improve the understanding and optimization of EICP treatment strategies. These findings have broader implications for environmental and geotechnical applications, including carbon storage, hydraulic control, and ground stabilization. Future studies should scale these methods to larger volumes, directly compare alternative injection strategies, and evaluate the long-term stability of CaCO₃ precipitates under variable environmental conditions.

Statements and Declarations

Supplementary Material

Supplementary material for this article is available online.

Acknowledgements

Simulations were performed on the ARCHIE-WeSt High Performance Computer (www.archie-west.ac.uk) based at the University of Strathclyde. The data analysis was supported by NERC NE/T00908X/1 and EPSRC EP/T023198/1, and data acquisition was supported by the NXCT (EP/T02593X) under their FaPOA scheme. PS is supported by the Centre for Doctoral Training (CDT) in Geoscience and the Low Carbon Energy Transition, and KJD was supported by NE/M018687/2.

Author Contributions

PS: Conceptualization, Methodology, Analysis, lead on all stages of MS preparation. JM: Funding, Data Acquisition, Supervision, Modelling, MS preparation. JW: Data acquisition, MS review. KD: Project design & funding, Analysis, Supervision, MS preparation.

Conflicts of Interest

The authors have no conflicts of interest to declare.

Data, Code & Protocol Availability

The data and analysis supporting the findings of this study are available from DOI: 10.5281/zenodo.14246214 https://doi.org/10.5281/zenodo.14246214

ORCID IDs

Philip J. Salter https://orcid.org/0009-0005-0731-5077

James M. Minto https://orcid.org/0000-0002-9414-4157

Jay Warnett https://orcid.org/0000-0003-2284-790X

Katherine J. Dobson https://orcid.org/0000-0003-2272-626X

References

1. Baum, D., Weaver, J., Zlotnikov, I., Knötel, D., Tomholt, L., Dean, M. (2019). High-Throughput Segmentation of Tiled Biological Structures using Random Walk Distance Transforms. Integrative and comparative biology, 59, 6. https://doi.org/10.1093/icb/icz117

2. Bernard, D., Guillon, O., Plougonven, E., & Combaret, N. (2011). Constrained sintering of glass films: Microstructure evolution assessed by synchrotron computed tomography. Acta Materialia, vol. 59, 6228-6238 https://doi.org/10.1016/j.actamat.2011.06.022

3. Carmona, J. P. S. F., Oliveira, P. J. V. & Lemos, L. J. L. (2016). Biostabilization of a Sandy Soil Using Enzymatic Calcium Carbonate Precipitation. Procedia Engineering, 143, 1301-1308. https://doi.org/10.1016/j.proeng.2016.06.144

4. Chedburn, L., Underhill, J. R., Head, S. & Jamieson, R. (2022). The critical evaluation of carbon dioxide subsurface storage sites: Geological challenges in the depleted fields of Liverpool Bay. AAPG Bulletin, 106, 1753-1789. https://doi.org/10.1306/07062221120

5. Cheng, L., Shahin, M. A. & Chu, J. (2018). Soil bio-cementation using a new one-phase low-pH injection method. Acta Geotechnica, 14, 615-626. https://doi.org/10.1007/s11440-018-0738-2

6. Chunxiang, Q., Jianyun, W., Ruixing, W., Liang, C. (2009). Corrosion protection of cement based building materials by surface deposition of CaCO3 by Bacillus pasteurii. Materials Science and Engineering: C, 29 (4), 1273–1280. https://doi.org/10.1016/j.msec.2008.10.025

7. Cui, M.-J., Lai, H.-J., Hoang, T. & Chu, J. (2020). One-phase-low-pH enzyme induced carbonate precipitation (EICP) method for soil improvement. Acta Geotechnica, 16, 481-489. https://doi.org/10.1007/s11440-020-01043-2

8. Dobson, K. J., Coban, S. B., McDonald, S. A., Walsh, J. N., Atwood, R. C. & Withers, P. J. (2016). 4-D imaging of sub-second dynamics in pore-scale processes using real-time synchrotron X-ray tomography. Solid Earth, 7, 1059-1073. https://doi.org/10.5194/se-7-1059-2016

9. Godinho, Ma, Chai, Storm & Burnett. (2019). Mineral Precipitation in Fractures and Nanopores within Shale Imaged Using Time-Lapse X-ray Tomography. Minerals, 9(8), 480. https://doi.org/10.3390/min9080480

10. Kim, D. H., Mahabadi, N., Jang, J. & Paassen, L. A. (2020). Assessing the Kinetics and Pore‐Scale Characteristics of Biological Calcium Carbonate Precipitation in Porous Media using a Microfluidic Chip Experiment. Water Resources Research, 56. https://doi.org/10.1029/2019WR025420

11. Konstantinou, C., Wang, Y., & Biscontin, G. (2023). A Systematic Study on the Influence of Grain Characteristics on Hydraulic and Mechanical Performance of MICP-Treated Porous Media. Transport in Porous Media, 147(2), 305-330. https://doi.org/10.1007/s11242-023-01909-5

12. Krevor, S., De Coninck, H., Gasda, S. E., Ghaleigh, N. S., De Gooyert, V., et al. (2023). Subsurface carbon dioxide and hydrogen storage for a sustainable energy future. Nature Reviews Earth & Environment, 4, 102-118. https://doi.org/10.1038/s43017-022-00376-8

13. Li, X., Tao, J. & van Paassen, L.A. (2024). Reactive transport modeling of microbial-induced calcite precipitation treatment through shallow underwater injection. Computers and Geotechnics, 174, 106601. https://doi.org/10.1016/j.compgeo.2024.106601

14. Lin, Q., Neethling, S. J., Dobson, K. J., Courtois, L. & Lee, P. D. (2015). Quantifying and minimising systematic and random errors in X-ray micro-tomography based volume measurements. Computers & Geosciences, 77, 1-7. https://doi.org/10.1016/j.cageo.2014.12.008

15. Menke, H. P., Reynolds, C. A., Andrew, M. G., Pereira Nunes, J. P., Bijeljic, B. & Blunt, M. J. (2018). 4D multi-scale imaging of reactive flow in carbonates: Assessing the impact of heterogeneity on dissolution regimes using streamlines at multiple length scales. Chemical Geology, 481, 27-37. https://doi.org/10.1016/j.chemgeo.2018.01.016

16. Minto, J. M., Hingerl, F. F., Benson, S. M. & Lunn, R. J. (2017). X-ray CT and multiphase flow characterization of a ‘bio-grouted’ sandstone core: The effect of dissolution on seal longevity. International Journal of Greenhouse Gas Control, 64, 152-162. https://doi.org/10.1016/j.ijggc.2017.07.007

17. Nemati, M. & G. Voordouw. (2003). Modification of porous media permeability, using calcium carbonate produced enzymatically in situ. Enzyme and Microbial Technology, 33, 635-642. https://doi.org/10.1016/S0141-0229(03)00191-1

18. Nemati, M., Greene, E. A. & Voordouw, G. (2005). Permeability profile modification using bacterially formed calcium carbonate: comparison with enzymic option. Process Biochemistry, 40, 925-933. https://doi.org/10.1016/j.procbio.2004.02.019

19. Otsu, N. (1979). A thresholding selection method from grayscale histogram. IEEE Transactions on Systems, Man, and Cybernetics, 9(1), 62-66. https://doi.org/10.1109/TSMC.1979.4310076

20. Peng, S., Di, H., Fan, L., Fan, W., & Qin, L. (2020). Factors Affecting Permeability Reduction of MICP for Fractured Rock. Frontiers in Earth Science, 8. https://doi.org/10.3389/feart.2020.00217

21. Putra, H., Yasuhara, H., Kinoshita, N., Neupane, D. & Lu, C. W. (2016). Effect of Magnesium as Substitute Material in Enzyme-Mediated Calcite Precipitation for Soil-Improvement Technique. Frontiers in Bioengineering and Biotechnology, 4, 37. http://dx.doi.org/10.3389/fbioe.2016.00037

22. Putra, H., Yasuhara, H., Kinoshita, N., Erizal & Sudibyo, T. (2018). Improving Shear Strength Parameters of Sandy Soil using Enzyme-Mediated Calcite Precipitation Technique. Civil Engineering Dimension, 20, 91-95. https://doi.org/10.9744/ced.20.2.91-95

23. Ringrose, P. S. & Meckel, T. A. (2019). Maturing global CO₂ storage resources on offshore continental margins to achieve 2DS emissions reductions. Scientific Reports, 9, 17944. https://doi.org/10.1038/s41598-019-54363-z

24. Schindelin, J., Arganda-Carreras, I., Frise, E., Kaynig, V., Longair, M., et al. (2012). Fiji: an open-source platform for biological-image analysis. Nature Methods, 9, 676-682. https://doi.org/10.1038/nmeth.2019

25. Singh, A., Paramkusam, B. R. & Maiti, P. R. (2021). Cyclic degradation and pore pressure dynamics of EICP treated hydrocarbon contaminated sands. Soil Dynamics and Earthquake Engineering, 140, 106369. https://doi.org/10.1016/j.soildyn.2020.106369

26. Studholme, C., Hill, D. L. G., Hawkes, D. J. (1999). An overlap invariant entropy measure of 3D medical image alignment. Pattern Recognition, Volume 32, Issue 1, 71-86. https://doi.org/10.1016/S0031-3203(98)00091-0

27. Wang, H., Sun, X., Miao, L., Cao, Z., Fan, G. & Wu, L. (2022). Induced CaCO₃ mineral formation based on enzymatical calcification for bioremediation under different pressure conditions. Journal of Petroleum Science and Engineering, 216, 110787. https://doi.org/10.1016/j.petrol.2022.110787

28. Weinhardt, F., Class, H., Dastjerdi, S. V., Karadimitriou, N., Lee, D., Steeb, H. (2021). Experimental Methods and Imaging for Enzymatically Induced Calcite Precipitation in a Microfluidic Cell. Water Resources Research. 57, 3, e2020WR029361. https://doi.org/10.1029/2020WR029361

29. Willems, C. J. L., Cheng, C., Watson, S. M., Minto, J., Williams, A., et al. (2021). Permeability and Mineralogy of the Újfalu Formation, Hungary, from Production Tests and Experimental Rock Characterization: Implications for Geothermal Heat Projects. Energies, 14, 4332. https://doi.org/10.3390/en14144332

30. Yang, Y., Chu, J., Liu, H. & Cheng, L. (2023). Improvement of uniformity of biocemented sand column using CH3COOH-buffered one-phase-low-pH injection method. Acta Geotechnica, 18, 413–428. https://doi.org/10.1007/s11440-022-01576-8

31. Yasuhara, H., Neupane, D., Hayashi, K., and Okamura, M. (2012). Experiments and predictions of physical properties of sand cemented by enzymatically-induced carbonate precipitation. Soils and Foundations, 52, 539–549. http://dx.doi.org/10.1016/j.sandf.2012.05.011