Anchored Physics-Informed Neural Network for Two-Phase Flow Simulation in Heterogeneous Porous Media

Jingqi Lin; Xia Yan; Kai Zhang; Zhao Zhang; Jun Yao

doi:10.69631/ipj.v2i3nr67

Authors

Jingqi Lin School of Petroleum Engineering, China University of Petroleum (East China), Qingdao, China; National Key Laboratory of Deep Oil and Gas, China University of Petroleum (East China), Qingdao, China https://orcid.org/0009-0001-4860-4036
Xia Yan School of Petroleum Engineering, China University of Petroleum (East China), Qingdao, China; National Key Laboratory of Deep Oil and Gas, China University of Petroleum (East China), Qingdao, China
Kai Zhang School of Petroleum Engineering, China University of Petroleum (East China), Qingdao, China; Civil Engineering School, Qingdao University of Technology, Qingdao, China https://orcid.org/0000-0002-6691-6762
Zhao Zhang Research Centre for Mathematics and Interdisciplinary Sciences, Shandong University, Qingdao, China https://orcid.org/0000-0003-0523-5071
Jun Yao School of Petroleum Engineering, China University of Petroleum (East China), Qingdao, China; National Key Laboratory of Deep Oil and Gas, China University of Petroleum (East China), Qingdao, China https://orcid.org/0000-0002-6720-584X

DOI:

https://doi.org/10.69631/ipj.v2i3nr67

Keywords:

Artificial intelligence for partial differential equations, AI4PDE, Simulation, Two-phase flow, Heterogeneous, Tensorizing, Adaptive architecture, Neural networks

Abstract

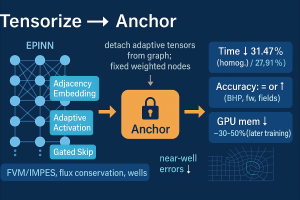
In this study, we propose a tensorization-anchoring strategy based on adaptive architectures to accelerate the computation of Enriched Physics-Informed Neural Networks (EPINN) for two-phase flow simulations. Specifically, we design an adaptive tensorization mechanism for the adjacency matrix embedding, the activation function, and the skip-gated connection in EPINN, which collectively expand the neural network's (NN) parameter space for learning more generalized patterns. Moreover, we developed an anchoring strategy by establishing Anchors-EPINN (An-EPINN). By detaching tensorization parameters from the computational graph and anchoring weighted nodes to fixed positions, the NN can benefit from tensorized fusion effects while reducing high-dimensional matrix calculations during forward and backward propagation, thereby enhancing simulation efficiency. This approach reduces execution time by 31.47% in homogeneous cases and 27.91% in heterogeneous cases, while maintaining higher computational accuracy.

Downloads

Download data is not yet available.

References

1. Anagnostopoulos, S. J., Toscano, J. D., Stergiopulos, N., & Karniadakis, G. E. (2024). Residual-based attention in physics-informed neural networks. Computer Methods in Applied Mechanics and Engineering, 421, 116805. https://doi.org/10.1016/j.cma.2024.116805

2. Ba, J. L., Kiros, J. R., & Hinton, G. E. (2016). Layer normalization (No. arXiv:1607.06450). arXiv. https://doi.org/10.48550/arXiv.1607.06450

3. Baydin, A. G., Pearlmutter, B. A., Radul, A. A., & Siskind, J. M. (2017). Automatic differentiation in machine learning: A survey. Journal of Machine Learning Research, 18(1), 5595–5637.

4. Brunton, S. L., & Kutz, J. N. (2024). Promising directions of machine learning for partial differential equations. Nature Computational Science, 4(7), 483–494. https://doi.org/10.1038/s43588-024-00643-2

5. Cai, S., Mao, Z., Wang, Z., Yin, M., & Karniadakis, G. E. (2021). Physics-informed neural networks (PINNs) for fluid mechanics: A review. Acta Mechanica Sinica, 37(12), 1727–1738. https://doi.org/10.1007/s10409-021-01148-1

6. Cen, J., & Zou, Q. (2024). Deep finite volume method for partial differential equations. Journal of Computational Physics, 517, 113307. https://doi.org/10.1016/j.jcp.2024.113307

7. Chen, C. L. P., & Liu, Z. (2018). Broad learning system: An effective and efficient incremental learning system without the need for deep architecture. IEEE Transactions on Neural Networks and Learning Systems, 29(1), 10–24. https://doi.org/10.1109/TNNLS.2017.2716952

8. Chen, H., Kou, J., Sun, S., & Zhang, T. (2019). Fully mass-conservative IMPES schemes for incompressible two-phase flow in porous media. Computer Methods in Applied Mechanics and Engineering, 350, 641–663. https://doi.org/10.1016/j.cma.2019.03.023

9. Chen, Z., Badrinarayanan, V., Lee, C.-Y., & Rabinovich, A. (2017). Gradnorm: Gradient normalization for adaptive loss balancing in deep multitask networks. https://doi.org/10.48550/ARXIV.1711.02257

10. Cuomo, S., Di Cola, V. S., Giampaolo, F., Rozza, G., Raissi, M., & Piccialli, F. (2022). Scientific machine learning through physics–informed neural networks: Where we are and what’s next. Journal of Scientific Computing, 92(3), 88. https://doi.org/10.1007/s10915-022-01939-z

11. Daw, A., Karpatne, A., Watkins, W., Read, J., & Kumar, V. (2017). Physics-guided neural networks (PGNN): An application in lake temperature modeling. arXiv. https://doi.org/10.48550/ARXIV.1710.11431

12. Delange, M., Aljundi, R., Masana, M., Parisot, S., Jia, X., et al. (2021). A continual learning survey: Defying forgetting in classification tasks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1–1. https://doi.org/10.1109/TPAMI.2021.3057446

13. Eymard, R., Gallouët, T., & Herbin, R. (2000). Finite volume methods. In Handbook of Numerical Analysis (Vol. 7, pp. 713–1018). Elsevier. https://doi.org/10.1016/S1570-8659(00)07005-8

14. Gou, J., Yu, B., Maybank, S. J., & Tao, D. (2021). Knowledge distillation: A survey. International Journal of Computer Vision, 129(6), 1789–1819. https://doi.org/10.1007/s11263-021-01453-z

15. Han, S., Mao, H., & Dally, W. J. (2015). Deep compression: Compressing deep neural networks with pruning, trained quantization and Huffman coding. arXiv. https://doi.org/10.48550/ARXIV.1510.00149

16. Ioffe, S., & Szegedy, C. (2015). Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv. https://doi.org/10.48550/ARXIV.1502.03167

17. Jagtap, A. D., Kawaguchi, K., & Karniadakis, G. E. (2020). Adaptive activation functions accelerate convergence in deep and physics-informed neural networks. Journal of Computational Physics, 404, 109136. https://doi.org/10.1016/j.jcp.2019.109136

18. Kendall, A., Gal, Y., & Cipolla, R. (2017). Multi-task learning using uncertainty to weigh losses for scene geometry and semantics. arXiv. https://doi.org/10.48550/ARXIV.1705.07115

19. Kingma, D. P., & Ba, J. (2017). Adam: A method for stochastic optimization (No. arXiv:1412.6980). arXiv. https://doi.org/10.48550/arXiv.1412.6980

20. Kumar, S. K. (2017). On weight initialization in deep neural networks (No. arXiv:1704.08863). arXiv. https://doi.org/10.48550/arXiv.1704.08863

21. LeCun, Y., Bengio, Y., & Hinton, G. (2015). Deep learning. Nature, 521(7553), 436–444. https://doi.org/10.1038/nature14539

22. Li, Z., Kovachki, N., Azizzadenesheli, K., Liu, B., Bhattacharya, K., Stuart, A., & Anandkumar, A. (2021). Fourier neural operator for parametric partial differential equations (No. arXiv:2010.08895). arXiv. https://doi.org/10.48550/arXiv.2010.08895

23. Lu, L., Jin, P., Pang, G., Zhang, Z., & Karniadakis, G. E. (2021). Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nature Machine Intelligence, 3(3), 218–229. https://doi.org/10.1038/s42256 -021-00302-5

24. Moortgat, J., & Firoozabadi, A. (2013). Three-phase compositional modeling with capillarity in heterogeneous and fractured media. SPE Journal, 18(06), 1150–1168. https://doi.org/10.2118/159777-PA

25. Novikov, A., Podoprikhin, D., Osokin, A., & Vetrov, D. (2015). Tensorizing neural networks. arXiv. https://doi.org/10.48550/ARXIV.1509.06569

26. Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., et al. (2019). PyTorch: An imperative style, high-performance deep learning library. arXiv. https://doi.org/10.48550/ARXIV.1912.01703

27. Peaceman, D. W. (1993). Representation of a horizontal well in numerical reservoir simulation. SPE Advanced Technology Series, 1(01), 7–16. https://doi.org/10.2118/21217-PA

28. Raissi, M., Perdikaris, P., & Karniadakis, G. E. (2019). Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 378, 686–707. https://doi.org/10.1016/j.jcp.2018.10.045

29. Uriarte, C., Pardo, D., & Omella, Á. J. (2022). A finite element based deep learning solver for parametric PDES. Computer Methods in Applied Mechanics and Engineering, 391, 114562. https://doi.org/10.1016/j.cma.2021.114562

30. Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., et al. (2017). Attention is all you need. arXiv. https://doi.org/10.48550/ARXIV.1706.03762

31. Wang, N., Chang, H., & Zhang, D. (2022). Surrogate and inverse modeling for two-phase flow in porous media via theory-guided convolutional neural network. Journal of Computational Physics, 466, 111419. https://doi.org/10.1016/j.jcp.2022.111419

32. Woo, S., Park, J., Lee, J.-Y., & Kweon, I. S. (2018). CBAM: Convolutional block attention module (No. arXiv:1807.06521). arXiv. https://doi.org/10.48550/arXiv.1807.06521

33. Wu, C., Zhu, M., Tan, Q., Kartha, Y., & Lu, L. (2023). A comprehensive study of non-adaptive and residual-based adaptive sampling for physics-informed neural networks. Computer Methods in Applied Mechanics and Engineering, 403, 115671. https://doi.org/10.1016/j.cma.2022.115671

34. Yan, X., Huang, Z., Yao, J., Li, Y., & Fan, D. (2016). An efficient embedded discrete fracture model based on mimetic finite difference method. Journal of Petroleum Science and Engineering, 145, 11–21. https://doi.org/10.1016/j.petrol.2016.03.013

35. Yan, X., Lin, J., Wang, S., Zhang, Z., Liu, P., et al. (2024). Physics-informed neural network simulation of two-phase flow in heterogeneous and fractured porous media. Advances in Water Resources, 189, 104731. https://doi.org/10.1016/j.advwatres.2024.104731

36. Yu, Y., Si, X., Hu, C., & Zhang, J. (2019). A review of recurrent neural networks: LSTM cells and network architectures. Neural Computation, 31(7), 1235–1270. https://doi.org/10.1162/neco_a_01199

37. Zhang, B. (2023). Nonlinear mode decomposition via physics-assimilated convolutional autoencoder for unsteady flows over an airfoil. Physics of Fluids, 35(9), 095115. https://doi.org/10.1063/5.0164250

38. Zhang, Z. (2022). A physics-informed deep convolutional neural network for simulating and predicting transient Darcy flows in heterogeneous reservoirs without labeled data. Journal of Petroleum Science and Engineering, 211, 110179. https://doi.org/10.1016/j.petrol.2022.110179

39. Zhang, Z., Yan, X., Liu, P., Zhang, K., Han, R., & Wang, S. (2023). A physics-informed convolutional neural network for the simulation and prediction of two-phase Darcy flows in heterogeneous porous media. Journal of Computational Physics, 477, 111919. https://doi.org/10.1016/j.jcp.2023.111919

40. Zhao, C., Zhang, F., Lou, W., Wang, X., & Yang, J. (2024). A comprehensive review of advances in physics-informed neural networks and their applications in complex fluid dynamics. Physics of Fluids, 36(10), 101301. https://doi.org/10.1063/5.0226562

41. Zhuang, F., Qi, Z., Duan, K., Xi, D., Zhu, Y., Zhu, H., Xiong, H., & He, Q. (2021). A comprehensive survey on transfer learning. Proceedings of the IEEE, 109(1), 43–76. https://doi.org/10.1109/JPROC.2020.3004555