Compaction-Induced Non-Monotonic Variation of Longitudinal Dispersion Coefficient in Granular Media

Yang Liu; Wenbo Gong; Han Xiao; Moran Wang

doi:10.69631/an65j282

Authors

Yang Liu Tsinghua University, Department of Engineering Mechanics, Beijing, China https://orcid.org/0009-0000-2300-9436
Wenbo Gong Tsinghua University, Department of Engineering Mechanics, Beijing, China
Han Xiao Tsinghua University, Department of Engineering Mechanics, Beijing, China
Moran Wang Tsinghua University, Department of Engineering Mechanics, Beijing, China https://orcid.org/0000-0002-0112-5150

DOI:

https://doi.org/10.69631/an65j282

Keywords:

Compaction, Dispersion coefficient, Pore network model, Porous media

Abstract

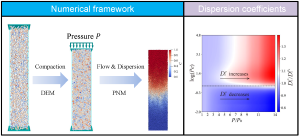
This study numerically investigates the impact of compaction on the longitudinal dispersion coefficient of granular materials by integrating the discrete element method with the pore network model. The results reveal a non-monotonic relationship between the dispersion coefficient and compaction. Specifically, the dispersion coefficient can decrease by up to 20% or increase by nearly 50% in magnitude. Furthermore, we define the variation in the dispersion coefficient, denoted as κ, which exhibits three distinct regimes across different Péclet numbers Pe. This non-monotonic behavior arises because compaction influences dispersion mechanisms in multiple ways. As the porous medium becomes more compact, the influence of molecular diffusion weakens, while both mechanical dispersion and hold-up dispersion intensify. This study identifies new sources and behaviors of hold-up dispersion that were not detected by classical dispersion theory. Specifically, hold-up dispersion arises in regions with weak flow, distinguishing it from zero-velocity zones, such as dead-ends or the interiors of permeable grains, as described in classical dispersion theories. Moreover, the newly identified hold-up dispersion is active only within intermediate ranges of Pe (10^-1<Pe<10^-3). The interplay between reduced molecular diffusion and enhanced hold-up and mechanical dispersion, along with shifts in dominant dispersion mechanisms across varying Pe, results in multiple regimes in the κ − Pe curve. Additionally, the study demonstrates that compaction alters the pore structure by reducing pore size and changing the topology of the pore network. However, changes in topology counteract the effects of reduced pore size by limiting the increase in flow disorder. Thus, the influence of compaction on dispersion is closely linked to mechanical physics. Our study provides unique insights into the structural design and modulation of the dispersion coefficient of porous materials.

Downloads

Download data is not yet available.

Author Biography

Moran Wang, Tsinghua University, Department of Engineering Mechanics, Beijing, China

Moran Wang is a Professor of Fluid Mechanics and Thermophysics at Tsinghua University. He obtained Bachelor and PhD degrees from Tsinghua University, and held postdoc positions in Johns Hopkins University and University of California of USA. He worked at Los Alamos National Laboratory as an Oppenheimer Fellow. He has been a full professor at Tsinghua University since 2011. He is working on micro/nanoscale fluid mechanics in porous media, multiscale modeling, nonlinear heat & mass transfer, and interfacial science. He has authored over 200 peer-reviewed papers on international journals which gained over 12,000 citations based on Google Scholar Reports (H-index: 55). Prof. Wang has been serving as editorial board members for several international journals including “International Journal of Mechanical Sciences”, “Energy Science and Engineering”, “Journal of Colloids and Interface Science”, “Transport in Porous Media”, “Journal of Porous Media” and so on. He has been invited to contribute comprehensive reviews on “Physics Reports”, “Material Science and Engineering R: Reports”, “Progress in Materials Science” and so on. He was awarded J.R. Oppenheimer Fellowship in 2008, Interpore P&G Award in 2019 and Fellow of IMMS in 2022.

References

1. Amooie, M. A., Soltanian, M. R., & Moortgat, J. (2018). Solutal convection in porous media: Comparison between boundary conditions of constant concentration and constant flux. Physical Review E, 98(3), 033118. https://doi.org/10.1103/PhysRevE.98.033118

2. Babaei, M., & Joekar-Niasar, V. (2016). A transport phase diagram for pore-level correlated porous media. Advances in Water Resources, 92, 23–29. https://doi.org/10.1016/j.advwatres.2016.03.014

3. Bear, J. (1988). Dynamics of fluids in porous media. Dover publications.

4. Bijeljic, B., & Blunt, M. J. (2007). Pore‐scale modeling of transverse dispersion in porous media. Water Resources Research, 43(12), 2006WR005700. https://doi.org/10.1029/2006WR005700

5. Bijeljic, B., Mostaghimi, P., & Blunt, M. J. (2011). Signature of non-Fickian solute transport in complex heterogeneous porous media. Physical Review Letters, 107(20), 204502. https://doi.org/10.1103/PhysRevLett.107.204502

6. Bijeljic, B., Muggeridge, A. H., & Blunt, M. J. (2004). Pore‐scale modeling of longitudinal dispersion. Water Resources Research, 40(11), 2004WR003567. https://doi.org/10.1029/2004WR003567

7. Bolster, D. (2014). The fluid mechanics of dissolution trapping in geologic storage of CO2. Journal of Fluid Mechanics, 740, 1–4. https://doi.org/10.1017/jfm.2013.531

8. Bonazzi, A., Jha, B., & De Barros, F. P. J. (2021). Transport analysis in deformable porous media through integral transforms. International Journal for Numerical and Analytical Methods in Geomechanics, 45(3), 307–324. https://doi.org/10.1002/nag.3150

9. Boon, M., Bijeljic, B., & Krevor, S. (2017). Observations of the impact of rock heterogeneity on solute spreading and mixing. Water Resources Research, 53(6), 4624–4642. https://doi.org/10.1002/2016WR019912

10. Bruderer, C., & Bernabé, Y. (2001). Network modeling of dispersion: Transition from Taylor Dispersion in homogeneous networks to mechanical dispersion in very heterogeneous ones. Water Resources Research, 37(4), 897–908. https://doi.org/10.1029/2000WR900362

11. Charlaix, E., Hulin, J. P., & Plona, T. J. (1987). Experimental study of tracer dispersion in sintered glass porous materials of variable compaction. The Physics of Fluids, 30(6), 1690–1698. https://doi.org/10.1063/1.866234

12. Chen, Z., Jin, X., & Wang, M. (2018). A new thermo-mechanical coupled DEM model with non-spherical grains for thermally induced damage of rocks. Journal of the Mechanics and Physics of Solids, 116, 54–69. https://doi.org/10.1016/j.jmps.2018.03.023

13. Cundall, P. A., & Strack, O. D. L. (1979). A discrete numerical model for granular assemblies. Géotechnique, 29(1), 47–65. https://doi.org/10.1680/geot.1979.29.1.47

14. Dentz, M., Hidalgo, J. J., & Lester, D. (2023). Mixing in porous media: Concepts and approaches across scales. Transport in Porous Media, 146(1–2), 5–53. https://doi.org/10.1007/s11242-022-01852-x

15. Dong, H., & Blunt, M. J. (2009). Pore-network extraction from micro-computerized-tomography images. Physical Review E, 80(3), 036307. https://doi.org/10.1103/PhysRevE.80.036307

16. Goirand, F., Le Borgne, T., & Lorthois, S. (2021). Network-driven anomalous transport is a fundamental component of brain microvascular dysfunction. Nature Communications, 12(1), 7295. https://doi.org/10.1038/s41467-021-27534-8

17. Goldobin, D. S. (2011). Scaling of transport coefficients of porous media under compaction. EPL (Europhysics Letters), 95(6), 64004. https://doi.org/10.1209/0295-5075/95/64004

18. Gong, W., Chen, Z., Lei, W., Zheng, J., Ju, Y., & Wang, M. (2024). Spontaneous imbibition in dual permeable media using dynamic pore network model. Journal of Geophysical Research: Solid Earth, 129(9), e2024JB029002. https://doi.org/10.1029/2024JB029002

19. Guéguen, Y., Palciauskas, V., & Guéguen, Y. (1994). Introduction to the physics of rocks. Princeton Univ. Press.

20. Hamamoto, S., Perera, M. S. A., Resurreccion, A., Kawamoto, K., Hasegawa, S., Komatsu, T., & Moldrup, P. (2009). The solute diffusion coefficient in variably compacted, unsaturated volcanic ash soils. Vadose Zone Journal, 8(4), 942–952. https://doi.org/10.2136/vzj2008.0184

21. Hulin, J. P., Charlaix, E., Plona, T. J., Oger, L., & Guyon, E. (1988). Tracer dispersion in sintered glass beads with a bidisperse size distribution. AIChE Journal, 34(4), 610–617. https://doi.org/10.1002/aic.690340410

22. Kandhai, D., Hlushkou, D., Hoekstra, A. G., Sloot, P. M. A., Van As, H., & Tallarek, U. (2002). Influence of stagnant zones on transient and asymptotic dispersion in macroscopically homogeneous porous media. Physical Review Letters, 88(23), 234501. https://doi.org/10.1103/PhysRevLett.88.234501

23. Kang, P. K., Lei, Q., Dentz, M., & Juanes, R. (2019). Stress‐induced anomalous transport in natural fracture networks. Water Resources Research, 55(5), 4163–4185. https://doi.org/10.1029/2019WR024944

24. Khan, Z. A., Agnaou, M., Sadeghi, M. A., Elkamel, A., & Gostick, J. T. (2021). Pore network modelling of galvanostatic discharge behaviour of lithium-ion battery cathodes. Journal of The Electrochemical Society, 168(7), 070534. https://doi.org/10.1149/1945-7111/ac120c

25. Khrapitchev, A. A., & Callaghan, P. T. (2003). Reversible and irreversible dispersion in a porous medium. Physics of Fluids, 15(9), 2649–2660. https://doi.org/10.1063/1.1596914

26. Koch, D. L., & Brady, J. F. (1985). Dispersion in fixed beds. Journal of Fluid Mechanics, 154, 399–427. https://doi.org/10.1017/S0022112085001598

27. Kumar, A., Jaiswal, D. K., & Kumar, N. (2009). Analytical solutions of one-dimensional advection-diffusion equation with variable coefficients in a finite domain. Journal of Earth System Science, 118(5), 539–549. https://doi.org/10.1007/s12040-009-0049-y

28. Kuncoro, P. H., Koga, K., Satta, N., & Muto, Y. (2014). A study on the effect of compaction on transport properties of soil gas and water I: Relative gas diffusivity, air permeability, and saturated hydraulic conductivity. Soil and Tillage Research, 143, 172–179. https://doi.org/10.1016/j.still.2014.02.006

29. Liu, F., & Wang, M. (2022). Phase diagram for preferential flow in dual permeable media. Journal of Fluid Mechanics, 948, A19. https://doi.org/10.1017/jfm.2022.649

30. Liu, Y., Gong, W., Xiao, H., & Wang, M. (2024a). A pore-scale numerical framework for solute transport and dispersion in porous media. Advances in Water Resources, 183, 104602. https://doi.org/10.1016/j.advwatres.2023.104602

31. Liu, Y., Gong, W., Xiao, H., & Wang, M. (2024b). Non-monotonic effect of compaction on longitudinal dispersion coefficient of porous media. Journal of Fluid Mechanics, 988, R2. https://doi.org/10.1017/jfm.2024.454

32. Liu, Y., Gong, W., Zhao, Y., Jin, X., & Wang, M. (2022). A pore‐throat segmentation method based on local hydraulic resistance equivalence for pore‐network modeling. Water Resources Research, 58(12), e2022WR033142. https://doi.org/10.1029/2022WR033142

33. Mehmani, Y., & Balhoff, M. T. (2015). Eulerian network modeling of longitudinal dispersion. Water Resources Research, 51(10), 8586–8606. https://doi.org/10.1002/2015WR017543

34. Molina, O., Vilarrasa, V., & Zeidouni, M. (2017). Geologic carbon storage for shale gas recovery. Energy Procedia, 114, 5748–5760. https://doi.org/10.1016/j.egypro.2017.03.1713

35. Morris, J. P., Hao, Y., Foxall, W., & McNab, W. (2011). A study of injection-induced mechanical deformation at the In Salah CO2 storage project. International Journal of Greenhouse Gas Control, 5(2), 270–280. https://doi.org/10.1016/j.ijggc.2010.10.004

36. Östergren, K. C. E., & Trägårdh, C. (2000). Characterization of hydrodynamic dispersion in a chromatographic column under compression. Chemical Engineering Journal, 79(2), 103–111. https://doi.org/10.1016/S1385-8947(00)00165-0

37. Patzek, T. W., & Silin, D. B. (2001). Shape factor and hydraulic conductance in noncircular capillaries. Journal of Colloid and Interface Science, 236(2), 295–304. https://doi.org/10.1006/jcis.2000.7413

38. Peters, G. P., & Smith, D. W. (2002). Solute transport through a deforming porous medium. International Journal for Numerical and Analytical Methods in Geomechanics, 26(7), 683–717. https://doi.org/10.1002/nag.219

39. Pfannkuch H. O. (1963), Contribution a I'etude des deplacement de fluids miscible dans un milieu poreux. [Contribution to the study of miscible fluid flow in porous media]. Revue de l'Institut Francais du Petrole [Journal of the French Petroleum Institute] 18(2), 215-270. https://search.worldcat.org/fr/title/Contribution-a-l%27etude-des-deplacements-de-fluides-miscibles-dans-un-milieu-poreux/oclc/460735531

40. Potyondy, D. O., & Cundall, P. A. (2004). A bonded-particle model for rock. International Journal of Rock Mechanics and Mining Sciences, 41(8), 1329–1364. https://doi.org/10.1016/j.ijrmms.2004.09.011

41. Puyguiraud, A., Gouze, P., & Dentz, M. (2019). Stochastic dynamics of lagrangian pore‐scale velocities in three‐dimensional porous media. Water Resources Research, 55(2), 1196–1217. https://doi.org/10.1029/2018WR023702

42. Puyguiraud, A., Gouze, P., & Dentz, M. (2021). Pore-scale mixing and the evolution of hydrodynamic dispersion in porous media. Physical Review Letters, 126(16), 164501. https://doi.org/10.1103/PhysRevLett.126.164501

43. Qiu, J., Chen, X., & Tong, J. (2022). Fully transient analytical solution for solute transport in 1D deforming saturated porous media considering nonlinear compressibility and permeability. Applied Mathematical Modelling, 108, 122–141. https://doi.org/10.1016/j.apm.2022.03.002

44. Ranjith, P. G., & Perera, M. S. A. (2011). A new triaxial apparatus to study the mechanical and fluid flow aspects of carbon dioxide sequestration in geological formations. Fuel, 90(8), 2751–2759. https://doi.org/10.1016/j.fuel.2011.04.004

45. Reynolds, A. M., Reavell, S. V., & Harral, B. B. (2000). Flow and dispersion through a close-packed fixed bed of spheres. Physical Review E, 62(3), 3632–3639. https://doi.org/10.1103/PhysRevE.62.3632

46. Ringrose, P. S., Mathieson, A. S., Wright, I. W., Selama, F., Hansen, O., Bissell, R., Saoula, N., & Midgley, J. (2013). The in salah CO2 storage project: Lessons learned and knowledge transfer. Energy Procedia, 37, 6226–6236. https://doi.org/10.1016/j.egypro.2013.06.551

47. Sahimi, M. (2011). Flow and transport in porous media and fractured rock: From classical methods to modern approaches (2nd ed). John Wiley & Sons, Incorporated.

48. Sahimi, M., Hughes, B. D., Scriven, L. E., & Ted Davis, H. (1986). Dispersion in flow through porous media—I. One-phase flow. Chemical Engineering Science, 41(8), 2103–2122. https://doi.org/10.1016/0009-2509(86)87128-7

49. Sahimi, M., & Imdakm, A. O. (1988). The effect of morphological disorder on hydrodynamic dispersion in flow through porous media. Journal of Physics A: Mathematical and General, 21(19), 3833–3870. https://doi.org/10.1088/0305-4470/21/19/019

50. Smith, D. W. (2000). One-dimensional contaminant transport through a deforming porous medium: Theory and a solution for a quasi-steady-state problem. International Journal for Numerical and Analytical Methods in Geomechanics, 24(8), 693–722. https://doi.org/10.1002/1096-9853(200007)24:8<693::AID-NAG91>3.0.CO;2-E

51. Tian, Z., Zhang, D., Zhou, G., Zhang, S., & Wang, M. (2023). Compaction and sintering effects on scaling law of permeability-porosity relation of powder materials. International Journal of Mechanical Sciences, 256, 108511. https://doi.org/10.1016/j.ijmecsci.2023.108511

52. Vaclav Smilauer, Angelidakis, V., Catalano, E., Caulk, R., Chareyre, B., et al. (2021). Yade documentation. Zenodo. https://doi.org/10.5281/ZENODO.5705394

53. Zhang, D., Tian, Z., Chen, Z., Wu, D., Zhou, G., et al. (2020). Compaction effects on permeability of spherical packing. Engineering Computations, 37(9), 3079–3096. https://doi.org/10.1108/EC-01-2020-0015

54. Zhu, W., Khirevich, S., & Patzek, T. W. (2021). Impact of fracture geometry and topology on the connectivity and flow properties of stochastic fracture networks. Water Resources Research, 57(7), e2020WR028652. https://doi.org/10.1029/2020WR028652