Static Elastic Properties of Rocks Obtained by X-ray Microtomography, Inverse Modeling and Surrogate Model

Ruan Gomes; Sergio Fontoura; Guilherme Righetto; Luiza Fernandes; Rafael Lopez; Rafaella Sampaio; Claudio Lima; Marcel  Naumann; William Silva

doi:10.69631/v65nzv74

Authors

Ruan Gomes Group of Technology in Energy and Petroleum – GTEP/PUC-Rio, Rio de Janeiro, Brazil; Oregon State University, Water Resources Graduate Program & Department of Biological & Ecological Engineering, Corvallis, Oregon, USA (Current); https://orcid.org/0000-0002-1376-0995
Sergio Fontoura Group of Technology in Energy and Petroleum – GTEP/PUC-Rio, Rio de Janeiro, Brazil; Pontifical Catholic University of Rio de Janeiro, Department of Civil and Environmental Engineering, Rio de Janeiro, Brazil
Guilherme Righetto Pontifical Catholic University of Rio de Janeiro, Department of Civil and Environmental Engineering, Rio de Janeiro, Brazil
Luiza Fernandes Pontifical Catholic University of Rio de Janeiro, Department of Civil and Environmental Engineering, Rio de Janeiro, Brazil https://orcid.org/0009-0003-4565-0517
Rafael Lopez Pontifical Catholic University of Rio de Janeiro, Department of Civil and Environmental Engineering, Rio de Janeiro, Brazil
Rafaella Sampaio Pontifical Catholic University of Rio de Janeiro, Department of Civil and Environmental Engineering, Rio de Janeiro, Brazil
Claudio Lima Equinor Research and Technology Center Rio, Rio de Janeiro, Brazil https://orcid.org/0009-0004-9003-1843
Marcel Naumann Equinor ASA, Stavanger, Norway https://orcid.org/0000-0002-9885-4295
William Silva Equinor Research and Technology Center Rio, Rio de Janeiro, Brazil https://orcid.org/0000-0003-1879-9386

DOI:

https://doi.org/10.69631/v65nzv74

Keywords:

Elastic properties, X-ray microtomography, Inverse modeling, Surrogate model, Pore-scale

Abstract

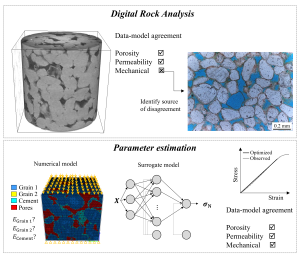
Digital rock analysis uses imaging techniques to obtain information concerning the internal structure of the rock. In the context of obtaining mechanical properties from digital images, much attention is given to determining the elastic parameters of rocks based on their mineralogical composition. While many applications for this type of simulation are available in the literature, the quantification of mineral property variations resulting from external influences has largely been overlooked. This work adopts an inverse modeling approach to estimate such elastic property variations in rocks. This methodology requires a predictive tool and an optimization algorithm to iteratively update the model’s parameters while reducing the discrepancies between modeled and measured data. In this study, a representative sandstone sample from the Botucatu Formation in Brazil was used to evaluate the methodology. Two case studies were considered: a synthetic example was designed for validation of the methodology while the second case applies real-world laboratory test data to estimate the properties that are most supported by the experimental evidence. A MATLAB code was built to integrate a finite element program and a genetic algorithm in a single framework. Additionally, an artificial neural network was used as a surrogate model to reduce the computational time of the numerical forward run. Overall, the results support the robustness of the approach and present a new alternative to obtain the mechanical properties of rock constituents at the pore scale.

Downloads

Download data is not yet available.

References

1. Abaqus (2014) Analysis User’s Manual, Version 6.14, Dassault Systems Simulia, Inc. https://www.scribd.com/document/517828704/Analysis-4

2. Andrä H, Combaret N, Dvorkin J, et al. (2013). Digital rock physics benchmarks - part II: Computing effective properties. Computer & Geosciences 50, 33–43. https://doi.org/10.1016/j.cageo.2012.09.008

3. Arns C, Knackstedt M, Pinczewski W, Garboczi E. (2002). Computation of linear elastic properties from microtomographic images: Methodology and agreement between theory and experiment. Geophysics 67, 1396–1405. https://doi.org/10.1190/1.1512785

4. Asher M, Croke B, Jakeman A, Peeters L. (2015). A review of surrogate models and their application to groundwater modeling. Water Resources Research 51, 5957–5973. https://doi.org/10.1002/2015WR016967

5. Bear J. (1972). Dynamics of Fluids in Porous Media. Dover Publications INC, New York, 800 pgs.

6. Bergstra J, Bengio Y. (2012). Random Search for Hyper-Parameter Optimization. Journal of Machine Learning Research 13, 281-305.

7. Cardoso O, Balaban R. (2015). Comparative study between Botucatu and Berea sandstone properties. Journal of South American Earth Sciences 62, 58–69. https://doi.org/10.1016/j.jsames.2015.04.004

8. Cartwright-Taylor A, Main I, Butler I, et al. (2020). Catastrophic failure: How and when? Insights from 4-D in situ x-ray microtomography. JGR Solid Earth 125, 8, e2020JB019642. https://doi.org/10.1029/2020JB019642

9. Cnudde V, Boone M. (2013). High-resolution X-ray computed tomography in geosciences: A review of the current technology and applications. Earth-Science Reviews 123, 1-17. https://doi.org/10.1016/j.earscirev.2013.04.003

10. Dong H, Blunt M. (2009). Pore-network extraction from micro-computerized-tomography images. Physical Review E 80, 036307. https://doi.org/10.1103/PhysRevE.80.036307

11. Ettermeyer F, Lechner P, Hofmann T, Andrä H, Schneider M, et al. (2019). Digital Sand Core Physics: Predicting physical properties of sand cores by simulations on digital microstructures. International Journal of Solids and Structures 188-189, 155–168. https://doi.org/10.1016/j.ijsolstr.2019.09.014

12. Faisal T, Awedalkarim A, Chevalier S, Jouini M, Sassi M. (2017). Direct scale comparison of numerical linear elastic moduli with acoustic experiments for carbonate rock X-ray CT scanned at multi-resolutions. Journal of Petroleum Science and Engineering 152, 653–663. https://doi.org/10.1016/j.petrol.2017.01.025

13. Faisal T, Islam A, Jouini M, Devarapalli R, Jouiad M, et al. (2019). Numerical prediction of carbonate elastic properties based on multi-scale imaging. Geomechanics for Energy and the Environment 20, 100125. https://doi.org/10.1016/j.gete.2019.100125

14. Ferreira L, Surmas R, Tonietto S, da Silva M, Peçanha R. (2020a). Modeling reactive flow on carbonates with realistic porosity and permeability fields. Advances in Water Resources 139, 103564. https://doi.org/10.1016/j.advwatres.2020.103564

15. Ferreira T, Rasband W. (2012). ImageJ user guide - IJ 1.46.r, National Institute of Health Bethesda, MD. https://imagej.net/ij/docs/guide/

16. Ferreira LP, Oliveira T, Surmas R, Silva M, Peçanha R. (2020b). Brinkman equation in reactive flow: Contribution of each term in carbonate acidification simulations. Advances in Water Resources 144, 103696. https://doi.org/10.1016/j.advwatres.2020.103696

17. Fu J, Thomas H, Li C. (2021). Tortuosity of porous media: Image analysis and physical simulation. Earth-Science Reviews 212, 103439. https://doi.org/10.1016/j.earscirev.2020.103439

18. Furtney J, Thielsen C, Le Goc R. (2022). Surrogate models in rock and soil mechanics: Integrating numerical modeling and machine learning. Rock Mechanics and Rock Engineering 55, 2845–2859. https://doi.org/10.1007/s00603-021-02720-8

19. Gerke K, Vasilyev RV, Khirevich S, et al. (2018). Finite-difference method Stokes solver (FDMSS) for 3D pore geometries: Software development, validation and case studies. Computers and Geosciences 114, 41–58. https://doi.org/10.1016/j.cageo.2018.01.005

20. Gerke K, Sizonenko TO, Karsanina M, Lavrukhin EV, Abashkin V, et al. (2020). Improving watershed-based pore-network extraction method using maximum inscribed ball pore-body positioning. Advances in Water Resources, 140, 103576. https://doi.org/10.1016/j.advwatres.2020.103576

21. David E. Goldberg. (1989). Genetic Algorithms in Search, Optimization and Machine Learning (1st. ed.). Addison-Wesley Longman Publishing Co., Inc., USA. https://dl.acm.org/doi/10.5555/534133

22. Gomes R, Gomes G, Vrugt J. (2022). A hybrid multi-step sensitivity-driven evolutionary polynomial regression enables robust model structure selection. Engineering Application of Artificial Intelligence 116, 105421. https://doi.org/10.1016/j.engappai.2022.105421

23. Gostick J. (2017). Versatile and efficient pore network extraction method using marker-based watershed segmentation. Physical Review E 96, 023307. https://doi.org/10.1103/PhysRevE.96.023307

24. Hernández-Pico R, Fontoura S, Righetto G, et al. (2014). Mechanical tests on digital samples of carbonates obtained using X-Ray microtomography, SBMR, VI Rock Mechanics Symposium, Goiania, Brazil.

25. Hussain M, Javadi A, Ahandar-Asr A, Farmani R. (2015). A surrogate model for simulation-optimization of aquifer systems subjected to seawater intrusion. Journal of Hydrology 523, 542–554. https://doi.org/10.1016/j.jhydrol.2015.01.079

26. Kim K, Zhuang L, Yang H, Kim H, Min K. (2015). Strength anisotropy of Berea sandstones: Results of X-Ray computed tomography, compression tests, and discrete modeling. Rock Mechanics and Rock Engineering 49, 1201–1210. https://doi.org/10.1007/s00603-015-0820-0

27. Lucas-Oliveira E, Araujo-Ferreira A, Trevizan W, dos Santos B, Bonagamba T. (2020). Sandstone surface relaxivity determined by NMR T2 distribution and digital rock simulation for permeability evaluation. Journal of Petroleum Science and Engineering 193, 107400. https://doi.org/10.1016/j.petrol.2020.107400

28. Marquardt D. (1963). An algorithm for least-squares estimation of nonlinear parameters. Journal of the Society for Industrial and Applied Mathematics 11, 2, 431–441. https://doi.org/10.1137/0111030

29. McBeck J, Aiken J, Ben-Zion Y, Renard F. (2020). Predicting the proximity to macroscopic failure using local strain populations from dynamic in situ X-ray tomography triaxial compression experiments on rocks. Earth and Planetary Science Letters 543, 116344. https://doi.org/10.1016/j.epsl.2020.116344

30. McBeck J, Kandula N, Aiken J, et al. (2019). Isolating the factors that govern fracture development in rocks throughout dynamic in situ X-Ray tomography experiments. Geophysical Research Letters 46, 20, 11127–11135. https://doi.org/10.1029/2019GL084613

31. McCulloch W, Pitts W. (1943). A logical calculus of the ideas immanent in nervous activity. The Bulletin of Mathematical Biology 5, 115–133

32. Montanheiro T, Artur A, Montanheiro F, Negri F, Gesicki A, et al. (2011). Investigação tecnológica de arenitos silicificados da formação Botucatu (NE do Paraná) para uso como rochas de revestimento [Technological investigation of silicified sandstones from the Botucatu Formation (NE Paraná) for use as cladding stone]. Geociências 30, 2, 237–251.

33. Narsilio G, Buzzi O, Fityus S, Yun T, Smith D. (2009). Upscaling of Navier-Stokes equation in porous media: Theoretical, numerical and experimental approach. Computer and Geotechnics 36, 7, 1200–1206. https://doi.org/10.1016/j.compgeo.2009.05.006

34. Njock P, Shen S, Zhou A, Modoni G. (2021). Artificial neural network optimized by differential evolution for predicting diameters of jet grouted columns. Journal of Rock Mechanics and Geotechnical Engineering 13, 6, 1500–1512. https://doi.org/10.1016/j.jrmge.2021.05.009

35. Oparaji U, Sheu RJ, Bankhead M, Austin J, Patelli E. (2017). Robust artificial neural network for reliability and sensitivity analyses of complex non-linear systems. Neural Networks 96, 80–90. https://doi.org/10.1016/j.neunet.2017.09.003

36. Saenger E, Enzmann F, Keehm Y, Steeb H. (2011). Digital rock physics: Effects of fluid viscosity on effective elastic properties. Journal of Applied Geophysics 74, 4, 236-241. https://doi.org/10.1016/j.jappgeo.2011.06.001

37. Saenger E, Lebedev M, Uribe D, Osorno M, Vialle S, et al. (2016). Analysis of high-resolution X-ray computed tomography images of Bentheim sandstone under elevated confining pressures. Geophysical Prospecting 64, 4, 848–859. https://doi.org/10.1111/1365-2478.12400

38. Schepp L, Ahrens B, Balcewicz M, et al. (2020). Digital rock physics and laboratory considerations on a high-porosity volcanic rock. Scientific Reports 10, 5840. https://doi.org/10.1038/s41598-020-62741-1

39. Scherer C, Lavina E. (2006). Stratigraphic evolution of a fluvial–eolian succession: The example of the Upper Jurassic—Lower Cretaceous Guará and Botucatu formations, Paraná basin, Southernmost Brazil. Gondwana Research 9, 4, 475–484. https://doi.org/10.1016/j.gr.2005.12.002

40. Schlüter S, Sheppard A, Brown K, Wildenschild D. (2014). Image processing of multiphase images obtained via X-ray microtomography: A review. Water Resources Research, 50, 4, 3615–3639. https://doi.org/10.1002/2014WR015256

41. Schön J. (2014). Physical Properties of Rocks. 2nd ed., Elsevier. Hardback ISBN: 9780081004043, eBook ISBN: 9780081004234. https://shop.elsevier.com/books/physical-properties-of-rocks/schon/978-0-08-100404-3

42. Seidl D, Valiveti D. (2022). Peridynamics and surrogate modeling of pressure-driven well stimulation. International Journal of Rock Mechanics and Mining Sciences 154, 105105. https://doi.org/10.1016/j.ijrmms.2022.105105

43. Shahin M. (2015). Use of evolutionary computing for modelling some complex problems in geotechnical engineering. Geomechanics and Geoengineering 10, 2, 109–125. https://doi.org/10.1080/17486025.2014.921333

44. Shang X, Liu Z, Zhang J, Lyu T, Zou Y. (2023). Tailoring the mechanical properties of 3D microstructures: A deep learning and genetic algorithm inverse optimization framework. Materials Today, 70, 71-81. https://doi.org/10.1016/j.mattod.2023.09.007

45. Singh A, Regenauer-Lieb K, Walsh S, Armstrong R, van Griethuysen J, et al. (2020). On Representative elementary volumes of grayscale micro-CT images of porous media. Geophysical Research Letters 47, 15. https://doi.org/10.1029/2020GL088594

46. Sun H, Belhaj H, Tao G, Vega S, Liu L. (2019). Rock properties evaluation for carbonate reservoir characterization with multi-scale digital rock images. Journal of Petroleum Science and Engineering 175, 654–664 https://doi.org/10.1016/j.petrol.2018.12.075

47. Synopsis, Inc. (2021). SimplewareTM ScanIP, version S-2021-06, Mountain View, USA. https://www.synopsys.com/content/dam/synopsys/simpleware/pdfs/simpleware-s2021-06-lifesciences.pdf

48. Vrugt J, Oliveira D, Schoups G, Diks C. (2022). On the use of distribution-adaptive likelihood functions: Generalized and universal likelihood functions, scoring rules and multi-criteria ranking. Journal of Hydrology 615, 128542. https://doi.org/10.1016/j.jhydrol.2022.128542

49. Vrugt J, Stauffer P, Wohling T, Robinson B, Vesselinov V. (2008). Inverse modeling of subsurface flow and transport properties: a review with new developments. Vadose Zone Journal 7, 2, 843–864. https://doi.org/10.2136/vzj2007.0078

50. Wang Y, Armstrong R, Mostaghimi P. (2019a). Enhancing resolution of digital rock images with super resolution convolutional neural networks. Journal of Petroleum Science and Engineering 182, 106261. https://doi.org/10.1016/j.petrol.2019.106261

51. Wang Y, Armstrong R, Mostaghimi P. (2019b). Boosting resolution and recovering texture of 2D and 3D micro-CT images with deep learning. Water Resources Research 56, 1. https://doi.org/10.1029/2019WR026052.

52. Wetzel M, Kempka T, Kuhn M. (2020). Hydraulic and mechanical impacts of pore space alterations within a sandstone quantified by a flow velocity-dependent precipitation approach. Materials 13 (14), 3100. https://doi.org/10.3390/ma13143100

53. Yang J, Liu Y, Yagiz S, Laouafa F. (2021). An intelligent procedure for updating deformation prediction of braced excavation in clay using gated recurrent unit neural networks. Journal of Rock Mechanics and Geotechnical Engineering 13, 6, 1485–1499. https://doi.org/10.1016/j.jrmge.2021.07.011